Atvirkštinės matricos adjungtinės matricos metodas. Atvirkštinės matricos radimas: trys algoritmai ir pavyzdžiai

Daugeliu savybių panašus į atvirkštinį.

Enciklopedinis „YouTube“.

1 / 5

✪ Kaip rasti atvirkštinę matricos vertę - bezbotvy

✪ Atvirkštinė matrica (2 būdai rasti)

✪ Atvirkštinė matrica Nr. 1

✪ 2015-01-28. Atvirkštinė 3x3 matrica

✪ 2015-01-27. Atvirkštinė matrica 2x2

Subtitrai

Atvirkštinės matricos savybės

det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), Kur det (\displaystyle \\det )žymi determinantą.
(A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1)) dviem kvadratinėms apverčiamoms matricoms A (\displaystyle A) Ir B (\displaystyle B).
(A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), Kur (. . .) T (\displaystyle (...)^(T))žymi transponuotą matricą.
(k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1)) bet kokiam koeficientui k ≠ 0 (\displaystyle k\not =0).
E − 1 = E (\displaystyle \E^(-1)=E).
Jei reikia išspręsti tiesinių lygčių sistemą, (b yra nulinis vektorius), kur x (\displaystyle x) yra norimas vektorius, o jei A − 1 (\displaystyle A^(-1)) tada egzistuoja x = A − 1 b (\displaystyle x=A^(-1)b). Priešingu atveju arba sprendinių erdvės matmuo yra didesnis už nulį, arba sprendinių visai nėra.

Atvirkštinės matricos radimo metodai

Jei matrica yra apverčiama, tada norėdami rasti atvirkštinę matricą, galite naudoti vieną iš šių metodų:

Tikslieji (tiesioginiai) metodai

Gauss-Jordan metodas

Paimkime dvi matricas: the A ir vienišas E. Pateikiame matricą A tapatybės matricai naudojant Gauss-Jordan metodą, taikant transformacijas išilgai eilučių (taip pat galite taikyti transformacijas išilgai stulpelių, bet ne maišyti). Pritaikę kiekvieną operaciją pirmajai matricai, taikykite tą pačią operaciją antrajai. Liejant pirmąją matricą į vienos rūšies bus baigtas, antroji matrica bus lygi A–1.

Naudojant Gauso metodą, pirmoji matrica kairėje bus padauginta iš vienos iš elementariųjų matricų Λ i (\displaystyle \Lambda _(i))(transvekcinė arba įstrižainė matrica su vienetais pagrindinėje įstrižainėje, išskyrus vieną padėtį):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Lambda A=E \RightArrow \Lambda =A^(-1)). Λ m = [ 1 … 0 − a 1 m / a m m 0 … 0 … 0 … 1 - a m - 1 m / a m m 0 … 0 0 … 0 1 / a m m 0 … 0 0 … 0 - a m + 1 m / a m m 1 … 0 … 0 … 0 − a n m / a m m 0 … 1 ] (\displaystyle \Lambda _(m)=(\begin(bmatrix)1&\dots &0&-a_(1m)/a_(mm)&0&\dots &0\\ &&&\taškai &&&\\0&\taškai &1&-a_(m-1m)/a_(mm)&0&\taškai &0\\0&\taškai &0&1/a_(mm)&0&\taškai &0\\0&\taškai &0&-a_( m+1m)/a_(mm)&1&\taškai &0\\&&&\taškai &&&\\0&\taškai &0&-a_(nm)/a_(mm)&0&\taškai &1\pabaiga(bmatrica))).

Antroji matrica pritaikius visas operacijas bus lygi Λ (\displaystyle\Lambda), tai yra, jis bus norimas. Algoritmo sudėtingumas - O (n 3) (\displaystyle O(n^(3))).

Naudojant algebrinę komplemento matricą

Matrica atvirkštinė matrica A (\displaystyle A), gali būti pavaizduotas formoje

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

Kur adj (A) (\displaystyle (\mbox(adj))(A))- adjungtinė matrica;

Algoritmo sudėtingumas priklauso nuo determinanto O det skaičiavimo algoritmo sudėtingumo ir yra lygus O(n²)·O det.

Naudojant LU/LUP skaidymą

Matricinė lygtis A X = I n (\displaystyle AX=I_(n)) atvirkštinei matricai X (\displaystyle X) galima laikyti kolekcija n (\displaystyle n) formos sistemos A x = b (\displaystyle Ax=b). Pažymėkime i (\displaystyle i) matricos stulpelis X (\displaystyle X) per X i (\displaystyle X_(i)); Tada A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ldots ,n),nes i (\displaystyle i) matricos stulpelis I n (\displaystyle I_(n)) yra vieneto vektorius e i (\displaystyle e_(i)). kitaip tariant, norint rasti atvirkštinę matricą, reikia išspręsti n lygčių su ta pačia matrica ir skirtingomis dešiniosiomis pusėmis. Atlikus LUP skaidymą (O(n³) laikas), kiekvienai iš n lygčių išspręsti reikia O(n²) laiko, taigi ir šiai darbo daliai reikia O(n³) laiko.

Jei matrica A yra ne vienaskaita, tada jai galima apskaičiuoti LUP skaidymą P A = L U (\displaystyle PA = LU). Leisti P A = B (\displaystyle PA = B), B – 1 = D (\displaystyle B^(-1) = D). Tada iš atvirkštinės matricos savybių galime parašyti: D = U – 1 L – 1 (\displaystyle D=U^(-1)L^(-1)). Jei šią lygybę padauginsite iš U ir L, galite gauti dvi formos lygybes U D = L − 1 (\displaystyle UD=L^(-1)) Ir D L = U − 1 (\displaystyle DL=U^(-1)). Pirmoji iš šių lygybių reiškia n² sistemą tiesines lygtis Dėl n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2))) iš kurių žinomos dešinės pusės (iš trikampių matricų savybių). Antrasis taip pat reiškia n² tiesinių lygčių sistemą n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2))) iš kurių žinomos dešinės pusės (taip pat iš trikampių matricų savybių). Kartu jie sudaro n² lygybių sistemą. Naudodami šias lygybes galime rekursyviai nustatyti visus n² matricos D elementus. Tada iš lygybės (PA) −1 = A −1 P −1 = B −1 = D. gauname lygybę A − 1 = D P (\displaystyle A^(-1) = DP).

Naudojant LU dekompoziciją, matricos D stulpelių permutacija nereikalinga, tačiau sprendimas gali skirtis, net jei matrica A yra ne vienaskaita.

Algoritmo sudėtingumas yra O(n³).

Iteraciniai metodai

Schultzo metodai

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),),\\U_() k+1)=U_(k)\suma _(i=0)^(n)\Psi _(k)^(i)\pabaiga(atvejai)))

Klaidos įvertinimas

Pradinio aproksimavimo pasirinkimas

Pradinės aproksimacijos pasirinkimo problema čia nagrinėjamuose iteraciniuose matricos inversijos procesuose neleidžia jų traktuoti kaip nepriklausomų universalių metodų, konkuruojančių su tiesioginės inversijos metodais, pagrįstais, pavyzdžiui, matricų LU skaidymu. Yra keletas rekomendacijų, kaip pasirinkti U 0 (\displaystyle U_(0)), užtikrinančios sąlygos įvykdymą ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (matricos spektrinis spindulys yra mažesnis už vienetą), kuris yra būtinas ir pakankamas proceso konvergencijai. Tačiau šiuo atveju pirmiausia reikia iš viršaus žinoti apverčiamosios matricos A arba matricos spektro įvertinimą. A A T (\displaystyle AA^(T))(būtent jei A yra simetriška teigiama apibrėžtoji matrica ir ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), tada galite pasiimti U 0 = α E (\displaystyle U_(0)=(\alpha )E), kur; jei A yra savavališka nevienetinė matrica ir ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), tada jie tiki U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), kur taip pat α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); Žinoma, galite supaprastinti situaciją ir pasinaudoti tuo ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), įdėti U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). Antra, tokiu būdu nurodant pradinę matricą, nėra garantijos, kad ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|) bus mažas (gal net pasirodys ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), o aukštas konvergencijos rodiklis nebus atskleistas iš karto.

Pavyzdžiai

Matrica 2x2

A − 1 = [ a b c d ] − 1 = 1 det (A) [ d − b − c a ] = 1 a d − b c [ d − b − c a ] . (\displaystyle \mathbf (A) ^(-1)=(\begin(bmatrix)a&b\\c&d\\\end(bmatrix))^(-1)=(\frac (1)(\det(\mathbf (A))))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrix))=(\frac (1)(ad- bc))(\begin(bmatrix)\,\,\,d&\!\!-b\\-c&\,a\\\end(bmatrica)).)

2x2 matricos inversija galima tik su sąlyga, kad a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).

Panagrinėkime atvirkštinės matricos daugybos operacijos apibrėžimo problemą.

Tegu A yra n eilės kvadratinė matrica. Matrica A^(-1), kartu su duota matrica A tenkina lygybes:

A^(-1)\cdot A=A\cdot A^(-1)=E,

paskambino atvirkščiai. Matrica A vadinama grįžtamasis, jei yra atvirkštinė reikšmė, kitaip - negrįžtamas.

Iš apibrėžimo matyti, kad jei atvirkštinė matrica A^(-1) egzistuoja, tai ji yra tos pačios eilės kvadratas kaip ir A. Tačiau ne kiekviena kvadratinė matrica turi atvirkštinę reikšmę. Jei matricos A determinantas lygus nuliui (\det(A)=0), tai jai atvirkštinės reikšmės nėra. Tiesą sakant, taikydami teoremą tapatumo matricos E=A^(-1)A matricų sandaugos determinantui, gauname prieštaravimą

\det(E)=\det(A^(-1)\cdot A)=\det(A^(-1))\det(A)=\det(A^(-1))\cdot0=0

kadangi tapatumo matricos determinantas yra lygus 1. Pasirodo, kad kvadratinės matricos nulis determinantas yra vienintelė atvirkštinės matricos egzistavimo sąlyga. Prisiminkite, kad kvadratinė matrica, kurios determinantas yra lygus nuliui, vadinama vienaskaita (vienaskaita), kitu atveju ji vadinama neišsigimusia (ne vienaskaita).

4.1 teorema apie atvirkštinės matricos egzistavimą ir unikalumą. Kvadratinė matrica A=\begin(pmatrix)a_(11)&\cdots&a_(1n)\\ \vtaškai&\dtaškai&\vtaškai\\ a_(n1)&\ctaškai&a_(nn) \end(pmatrica), kurio determinantas yra ne nulis, turi atvirkštinę matricą ir, be to, tik vieną:

A^(-1)=\frac(1)(\det(A))\cdot\! \begin(pmatrix)A_(11)&A_(21)&\cdots&A_(1n)\\ A_(12)&A_(22)&\cdots&A_(n2)\\ \vtaškai&\vtaškai&\dtaškai&\vtaškai\\ A_(1n) )&A_(2n)&\cdots&A_(nn) \end(pmatrix)= \frac(1)(\det(A))\cdot A^(+),

kur A^(+) yra matrica, transponuota matricai, sudarytai iš matricos A elementų algebrinių komplementų.

Matrica A^(+) vadinama adjunktinė matrica matricos A atžvilgiu.

Tiesą sakant, matrica \frac(1)(\det(A))\,A^(+) egzistuoja su sąlyga \det(A)\ne0 . Būtina parodyti, kad jis yra atvirkštinis A, t.y. atitinka dvi sąlygas:

\begin(aligned)\mathsf(1))&~A\cdot\!\left(\frac(1)(\det(A))\cdot A^(+)\right)=E;\\ \mathsf (2))&~ \!\left(\frac(1)(\det(A))\cdot A^(+)\right)\!\cdot A=E.\end(sulygiuotas)

Įrodykime pirmąją lygybę. Pagal 2.3 pastabų 4 punktą iš determinanto savybių išplaukia, kad AA^(+)=\det(A)\cdot E. Štai kodėl

A\cdot\!\left(\frac(1)(\det(A))\cdot A^(+)\right)= \frac(1)(\det(A))\cdot AA^(+) = \frac(1)(\det(A))\cdot \det(A)\cdot E=E,

ką ir reikėjo parodyti. Antroji lygybė įrodoma panašiai. Todėl, esant sąlygai \det(A)\ne0, matrica A turi atvirkštinę reikšmę

A^(-1)=\frac(1)(\det(A))\cdot A^(+).

Atvirkštinės matricos unikalumą įrodysime prieštaravimu. Tegul, be matricos A^(-1), yra dar viena atvirkštinė matrica B\,(B\ne A^(-1)), kad AB=E. Padauginę abi šios lygybės puses iš kairės iš matricos A^(-1) , gauname \underbrace(A^(-1)AB)_(E)=A^(-1)E. Taigi B=A^(-1) , o tai prieštarauja prielaidai B\ne A^(-1) . Todėl atvirkštinė matrica yra unikali.

Pastabos 4.1

1. Iš apibrėžimo matyti, kad matricos A ir A^(-1) keičiasi.

2. Ne vienaskaitos įstrižainės matricos atvirkštinė vertė taip pat yra įstrižainė:

\Bigl[\operatoriaus vardas(diag)(a_(11),a_(22),\ldots,a_(nn))\Bigr]^(-1)= \operatoriaus vardas(diag)\!\left(\frac(1) )(a_(11)),\,\frac(1)(a_(22)),\,\ldots,\,\frac(1)(a_(nn))\right)\!.

3. Nevienaskaitės apatinės (viršutinės) trikampės matricos atvirkštinė vertė yra apatinė (viršutinė) trikampė.

4. Elementariosios matricos turi atvirkštines vertes, kurios taip pat yra elementarios (žr. 1.11 pastabų 1 pastraipą).

Atvirkštinės matricos savybės

Matricos inversijos operacija turi šias savybes:

\begin (lygiuotas)\bold(1.)&~~ (A^(-1))^(-1)=A\,;\\ \bold(2.)&~~ (AB)^(-1 )=B^(-1)A^(-1)\,;\\ \bold(3.)&~~ (A^T)^(-1)=(A^(-1))^T\ ,;\\ \bold(4.)&~~ \det(A^(-1))=\frac(1)(\det(A))\,;\\ \bold(5.)&~~ E^(-1)=E\,. \pabaiga (sulygiuota)

jei 1-4 lygybėse nurodyti veiksmai turi prasmę.

Įrodykime 2 savybę: jei tos pačios eilės vienaskaitos kvadratinių matricų sandauga AB turi atvirkštinę matricą, tai (AB)^(-1)=B^(-1)A^(-1).

Iš tiesų, matricų AB sandaugos determinantas nėra lygus nuliui, nes

\det(A\cdot B)=\det(A)\cdot\det(B), Kur \det(A)\ne0,~\det(B)\ne0

Todėl atvirkštinė matrica (AB)^(-1) egzistuoja ir yra unikali. Pagal apibrėžimą parodykime, kad matrica B^(-1)A^(-1) yra atvirkštinė matricai AB. Tikrai.

Ši tema yra viena nekenčiamiausių tarp studentų. Blogiau, ko gero, yra kvalifikacijos.

Apgaulė ta, kad pati atvirkštinio elemento sąvoka (kalbu ne tik apie matricas) nurodo daugybos operaciją. Netgi mokyklos mokymo programa Daugyba laikoma sudėtinga operacija, o matricų daugyba paprastai yra atskira tema, kuriai skiriu visą pastraipą ir vaizdo pamoką.

Šiandien nesigilinsime į matricos skaičiavimo detales. Tiesiog prisiminkime: kaip žymimos matricos, kaip jos dauginamos ir kas iš to išplaukia.

Apžvalga: Matricos daugyba

Pirmiausia susitarkime dėl žymėjimo. $A$ dydžio matrica $\left[ m\times n \right]$ yra tiesiog skaičių lentelė su tiksliai $m$ eilučių ir $n$ stulpelių:

\=\underbrace(\left[ \begin(matrica) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & (a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\pabaiga (matrica) \right])_(n)\]

Kad netyčia nesupainiotumėte eilučių ir stulpelių (patikėkite, egzamine galite supainioti vieną su dviem, jau nekalbant apie kai kurias eilutes), tiesiog pažiūrėkite į paveikslėlį:

Matricinių ląstelių indeksų nustatymas

Kas vyksta? Jei įdėsite standartinę koordinačių sistemą $OXY$ viršutiniame kairiajame kampe ir nukreipsite ašis taip, kad jos apimtų visą matricą, tada kiekvienas šios matricos langelis gali būti unikaliai susietas su koordinatėmis $\left(x;y \right)$ - tai bus eilutės ir stulpelio numeris.

Kodėl koordinačių sistema yra viršutiniame kairiajame kampe? Taip, nes nuo ten mes pradedame skaityti bet kokius tekstus. Tai labai lengva prisiminti.

Kodėl $x$ ašis nukreipta žemyn, o ne į dešinę? Vėlgi, viskas paprasta: paimkite standartinę koordinačių sistemą ($x$ ašis eina į dešinę, $y$ – aukštyn) ir pasukite ją taip, kad ji apimtų matricą. Tai sukimasis 90 laipsnių pagal laikrodžio rodyklę – rezultatą matome paveikslėlyje.

Apskritai, mes supratome, kaip nustatyti matricos elementų indeksus. Dabar pažiūrėkime į dauginimą.

Apibrėžimas. Matricos $A=\left[ m\times n \right]$ ir $B=\left[ n\times k \right]$, kai pirmojo stulpelių skaičius sutampa su antrosios eilučių skaičiumi vadinamas nuosekliu.

Būtent tokia tvarka. Galima susipainioti ir pasakyti, kad matricos $A$ ir $B$ sudaro tvarkingą porą $\left(A;B \right)$: jei jos yra nuoseklios šia tvarka, tai visai nebūtina, kad $B $ ir $ A $ tuos. pora $\left(B;A \right)$ taip pat yra nuosekli.

Galima padauginti tik suderintas matricas.

Apibrėžimas. Atitinkamų matricų $A=\left[ m\times n \right]$ ir $B=\left[ n\times k \right]$ sandauga yra nauja matrica$C=\left[ m\times k \right]$, kurio elementai $((c)_(ij))$ apskaičiuojami pagal formulę:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Kitaip tariant: norint gauti matricos $C=A\cdot B$ elementą $((c)_(ij))$, reikia paimti pirmosios matricos $i$ eilutę, $j$ - antrosios matricos stulpelį, tada padauginkite poromis elementus iš šios eilutės ir stulpelio. Sudėkite rezultatus.

Taip, tai toks griežtas apibrėžimas. Iš karto išplaukia keli faktai:

Matricos daugyba, paprastai kalbant, yra nekomutacinė: $A\cdot B\ne B\cdot A$;
Tačiau daugyba yra asociatyvi: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
Ir netgi pagal paskirstymą: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
Ir dar kartą pagal paskirstymą: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Daugybos pasiskirstymas turėjo būti aprašytas atskirai kairiajam ir dešiniajam sumos koeficientui būtent dėl daugybos operacijos nekomutaciškumo.

Jei paaiškėja, kad $A\cdot B=B\cdot A$, tokios matricos vadinamos komutacinėmis.

Tarp visų matricų, kurios yra padaugintos iš kažko, yra specialių - tų, kurias padauginus iš bet kurios matricos $A$, vėl gaunama $A$:

Apibrėžimas. Matrica $E$ vadinama tapatybe, jei $A\cdot E=A$ arba $E\cdot A=A$. Kvadratinės matricos $A$ atveju galime parašyti:

Tapatybės matrica yra dažnas svečias sprendžiant matricos lygtis. Ir apskritai dažnas svečias matricų pasaulyje. :)

Ir dėl šito $E$ kažkas sugalvojo visas nesąmones, kurios bus parašytos toliau.

Kas yra atvirkštinė matrica

Kadangi matricos daugyba yra labai daug darbo reikalaujanti operacija (tenka padauginti krūvą eilučių ir stulpelių), atvirkštinės matricos sąvoka taip pat pasirodo ne pati trivialiausia. Ir reikalauja tam tikro paaiškinimo.

Rakto apibrėžimas

Na, laikas sužinoti tiesą.

Apibrėžimas. Matrica $B$ vadinama atvirkštine matricos $A$, jei

Atvirkštinė matrica žymima $((A)^(-1))$ (nepainioti su laipsniu!), todėl apibrėžimą galima perrašyti taip:

Atrodytų, viskas labai paprasta ir aišku. Tačiau analizuojant šį apibrėžimą iškart kyla keletas klausimų:

Ar atvirkštinė matrica visada egzistuoja? Ir jei ne visada, tai kaip nustatyti: kada ji egzistuoja, o kada ne?
O kas sakė, kad tokia matrica yra būtent viena? O jei kokiai nors pradinei matricai $A$ yra visa minia atvirkštinių?
Kaip atrodo visi šie „atvirkščiai“? Ir kaip tiksliai turėtume juos suskaičiuoti?

Kalbant apie skaičiavimo algoritmus, apie tai kalbėsime šiek tiek vėliau. Tačiau į likusius klausimus atsakysime dabar. Suformuluokime juos atskirų teiginių-lemų pavidalu.

Pagrindinės savybės

Pradėkime nuo to, kaip iš principo turėtų atrodyti matrica $A$, kad jai egzistuotų $((A)^(-1))$. Dabar įsitikinsime, kad abi šios matricos turi būti kvadratinės ir vienodo dydžio: $\left[ n\times n \right]$.

1 lema. Duota matrica $A$ ir jos atvirkštinė $((A)^(-1))$. Tada abi šios matricos yra kvadratinės ir tos pačios eilės $n$.

Įrodymas. Tai paprasta. Tegul matrica $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Kadangi produktas $A\cdot ((A)^(-1))=E$ egzistuoja pagal apibrėžimą, matricos $A$ ir $((A)^(-1))$ yra nuoseklios nurodyta tvarka:

\[\begin(lygiuoti) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( lygiuoti)\]

Tai tiesioginė matricos daugybos algoritmo pasekmė: koeficientai $n$ ir $a$ yra „tranzitiniai“ ir turi būti lygūs.

Tuo pačiu apibrėžiamas ir atvirkštinis daugyba: $((A)^(-1))\cdot A=E$, todėl matricos $((A)^(-1))$ ir $A$ yra taip pat atitinka nurodyta tvarka:

\[\begin (lygiuoti) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( lygiuoti)\]

Taigi, neprarasdami bendrumo, galime daryti prielaidą, kad $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Tačiau pagal $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$ apibrėžimą, todėl matricų dydžiai griežtai sutampa:

\[\begin (lygiuoti) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end (lygiuoti)\]

Taigi paaiškėja, kad visos trys matricos – $A$, $((A)^(-1))$ ir $E$ – yra $\left[ n\times n \right]$ dydžio kvadratinės matricos. Lema įrodyta.

Na, tai jau gerai. Matome, kad tik kvadratinės matricos yra apverčiamos. Dabar įsitikinkime, kad atvirkštinė matrica visada yra ta pati.

2 lema. Duota matrica $A$ ir jos atvirkštinė $((A)^(-1))$. Tada ši atvirkštinė matrica yra vienintelė.

Įrodymas. Eikime prie prieštaravimo: tegul matrica $A$ turi bent dvi atvirkštines vertes – $B$ ir $C$. Tada pagal apibrėžimą yra teisingos šios lygybės:

\[\begin(lygiuoti) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(lygiuoti)\]

Iš 1 lemos darome išvadą, kad visos keturios matricos – $A$, $B$, $C$ ir $E$ – yra tos pačios eilės kvadratai: $\left[ n\times n \right]$. Todėl produktas apibrėžiamas:

Kadangi matricos daugyba yra asociatyvi (bet ne komutacinė!), galime rašyti:

\[\begin(lygiuoti) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rodyklė dešinėn B=C. \\ \end(lygiuoti)\]

Gavome vienintelį įmanomą variantą: dvi atvirkštinės matricos kopijos yra lygios. Lema įrodyta.

Aukščiau pateikti argumentai beveik pažodžiui pakartoja atvirkštinio elemento unikalumo įrodymą visiems realiesiems skaičiams $b\ne 0$. Vienintelis reikšmingas papildymas yra matricų matmenų įvertinimas.

Tačiau mes vis dar nieko nežinome, ar kiekviena kvadratinė matrica yra apverčiama. Čia mums į pagalbą ateina determinantas – tai pagrindinė visų kvadratinių matricų charakteristika.

3 lema. Duota matrica $A$. Jei jos atvirkštinė matrica $((A)^(-1))$ egzistuoja, tada pradinės matricos determinantas yra nulis:

\[\left| A\right|\ne 0\]

Įrodymas. Jau žinome, kad $A$ ir $((A)^(-1))$ yra $\left[ n\times n \right]$ dydžio kvadratinės matricos. Todėl kiekvienam iš jų galime apskaičiuoti determinantą: $\left| A\right|$ ir $\left| ((A)^(-1)) \right|$. Tačiau produkto determinantas yra lygus determinantų sandaugai:

\[\left| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \right|\]

Bet pagal apibrėžimą $A\cdot ((A)^(-1))=E$, o $E$ determinantas visada lygus 1, taigi

\[\begin(lygiuoti) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E\right|; \\ & \left| A \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \end(lygiuoti)\]

Dviejų skaičių sandauga yra lygi vienetui tik tuo atveju, jei kiekvienas iš šių skaičių yra ne nulis:

\[\left| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Taigi paaiškėja, kad $\left| A \right|\ne 0$. Lema įrodyta.

Tiesą sakant, šis reikalavimas yra gana logiškas. Dabar išanalizuosime atvirkštinės matricos paieškos algoritmą – ir bus visiškai aišku, kodėl su nuliniu determinantu atvirkštinė matrica iš esmės negali egzistuoti.

Tačiau pirmiausia suformuluokime „pagalbinį“ apibrėžimą:

Apibrėžimas. Vienaskaita matrica yra kvadratinė matrica, kurios dydis yra $\left[n\times n \right]$, kurios determinantas yra nulis.

Taigi galime teigti, kad kiekviena apverčiama matrica yra ne vienaskaita.

Kaip rasti atvirkštinę matricos vertę

Dabar apsvarstysime universalų atvirkštinių matricų paieškos algoritmą. Apskritai yra du visuotinai pripažinti algoritmai, šiandien taip pat apsvarstysime antrąjį.

Ta, kuri bus aptarta dabar, yra labai efektyvi matricoms, kurių dydis yra $\left[ 2\time 2 \right]$ ir – iš dalies – dydis $\left[3\time 3 \right]$. Bet pradedant nuo dydžio $\left[ 4\time 4 \right]$, geriau jo nenaudoti. Kodėl – dabar viską suprasite patys.

Algebriniai priedai

Pasiruošk. Dabar bus skausmas. Ne, nesijaudink: graži seselė su sijonu, kojinėmis su nėriniais neateis ir nesušvirkš į sėdmenis. Viskas daug proziškesnė: pas jus ateina algebriniai papildymai ir Jos Didenybė „Sąjungos matrica“.

Pradėkime nuo pagrindinio dalyko. Tegu yra $A=\left[ n\times n \right]$ dydžio kvadratinė matrica, kurios elementai vadinami $((a)_(ij))$. Tada kiekvienam tokiam elementui galime apibrėžti algebrinį papildinį:

Apibrėžimas. Algebrinis papildinys $((A)_(ij))$ elementui $((a)_(ij))$, esančiam $i$-oje eilutėje ir $j$-oje matricos $A=\left[ n \times n \right]$ yra formos konstrukcija

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Kur $M_(ij)^(*)$ yra matricos, gautos iš pradinio $A$, išbraukus tą pačią $i$-ąją eilutę ir $j$-ąją stulpelį, determinantas.

Vėlgi. Matricos elemento su koordinatėmis $\left(i;j \right)$ algebrinis papildymas žymimas $((A)_(ij))$ ir apskaičiuojamas pagal schemą:

Pirmiausia iš pradinės matricos ištriname $i$ eilutę ir $j$-tą stulpelį. Gauname naują kvadratinę matricą ir jos determinantą pažymime kaip $M_(ij)^(*)$.
Tada šį determinantą padauginame iš $((\left(-1 \right))^(i+j))$ – iš pradžių ši išraiška gali atrodyti pribloškianti, bet iš esmės mes tiesiog išsiaiškiname ženklą priešais $M_(ij)^(*) $.
Suskaičiuojame ir gauname konkretų skaičių. Tie. algebrinis sudėjimas yra būtent skaičius, o ne kokia nors nauja matrica ir pan.

Pati matrica $M_(ij)^(*)$ vadinama elemento $((a)_(ij))$ papildoma minora. Ir šia prasme aukščiau pateiktas algebrinio papildinio apibrėžimas yra ypatingas sudėtingesnio apibrėžimo atvejis – tai, ką mes apžvelgėme pamokoje apie determinantą.

Svarbi pastaba. Tiesą sakant, „suaugusiųjų“ matematikoje algebriniai priedai apibrėžiami taip:

Kvadratinėje matricoje paimame $k$ eilutes ir $k$ stulpelius. Jų sankirtoje gauname $\left[ k\times k \right]$ dydžio matricą - jos determinantas vadinamas $k$ eilės minora ir žymimas $((M)_(k))$.

Tada išbraukiame šias „pasirinktas“ $k$ eilutes ir $k$ stulpelius. Dar kartą gauname kvadratinę matricą – jos determinantas vadinamas papildomu mažuoju ir žymimas $M_(k)^(*)$.

Padauginkite $M_(k)^(*)$ iš $((\left(-1 \right)))^(t))$, kur $t$ yra (dėmesio dabar!) visų pasirinktų eilučių skaičių suma ir stulpeliai . Tai bus algebrinis papildymas.

Pažvelkite į trečiąjį žingsnį: iš tikrųjų yra 2 000 USD terminų suma! Kitas dalykas yra tai, kad $k=1$ gausime tik 2 terminus - tai bus tie patys $i+j$ - elemento $((a)_(ij)) $, kuriam mes esame "koordinatės". ieško algebrinio papildinio.

Taigi šiandien mes naudojame šiek tiek supaprastintą apibrėžimą. Bet kaip matysime vėliau, to bus daugiau nei pakankamai. Daug svarbesnis yra šis dalykas:

Apibrėžimas. Sąjunginė matrica $S$ su kvadratine matrica $A=\left[ n\times n \right]$ yra nauja $\left[ n\times n \right]$ dydžio matrica, gaunama iš $A$ pakeičiant $(( a)_(ij))$ algebriniais priedais $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrica) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\pabaiga (matrica) \right]\]

Pirmoji mintis, kylanti suvokus šį apibrėžimą, yra „kiek reikės suskaičiuoti! Atsipalaiduokite: teks skaičiuoti, bet ne tiek daug. :)

Na, visa tai labai gražu, bet kam to reikia? Bet kodėl.

Pagrindinė teorema

Grįžkime šiek tiek atgal. Atminkite, kad 3 lemoje buvo nurodyta, kad apverčiamoji matrica $A$ visada yra ne vienaskaita (ty jos determinantas yra ne nulis: $\left| A \right|\ne 0$).

Taigi, yra ir priešingai: jei matrica $A$ nėra vienaskaita, ji visada yra apverčiama. Ir netgi yra $((A)^(-1))$ paieškos schema. Pasižiūrėk:

Atvirkštinės matricos teorema. Tegu duota kvadratinė matrica $A=\left[ n\times n \right]$, o jos determinantas nėra nulis: $\left| A \right|\ne 0$. Tada egzistuoja atvirkštinė matrica $((A)^(-1))$ ir apskaičiuojama pagal formulę:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

O dabar – viskas taip pat, tik įskaitoma rašysena. Norėdami rasti atvirkštinę matricą, jums reikia:

Apskaičiuokite determinantą $\left| A \right|$ ir įsitikinkite, kad jis nėra nulis.
Sukonstruoti sąjungos matricą $S$, t.y. suskaičiuokite 100500 algebrinių priedų $((A)_(ij))$ ir įdėkite juos į vietą $((a)_(ij))$.
Perkelkite šią matricą $S$ ir padauginkite ją iš kažkokio skaičiaus $q=(1)/(\left| A \right|)\;$.

Tai viskas! Rasta atvirkštinė matrica $((A)^(-1))$. Pažiūrėkime į pavyzdžius:

\[\left[ \begin(matrica) 3 & 1 \\ 5 & 2 \\\end(matrica) \right]\]

Sprendimas. Patikrinkime grįžtamumą. Apskaičiuokime determinantą:

\[\left| A\right|=\left| \begin(matrica) 3 & 1 \\ 5 & 2 \\\end(matrica) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Determinantas skiriasi nuo nulio. Tai reiškia, kad matrica yra apverčiama. Sukurkime sąjungos matricą:

Apskaičiuokime algebrinius priedus:

\[\begin(lygiuoti) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2 \right|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5 \right|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\dešinė|=3. \\ \end(lygiuoti)\]

Atkreipkite dėmesį: determinantai |2|, |5|, |1| ir |3| yra $\left[ 1\times 1 \right]$ dydžio matricų determinantai, o ne moduliai. Tie. jei įtraukiami kvalifikaciniai rodikliai neigiami skaičiai, nereikia pašalinti „minuso“.

Iš viso mūsų sąjungos matrica atrodo taip:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(masyvas)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(masyvas) \right])^(T))=\left[ \begin (masyvas)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(masyvas) \right]\]

Gerai, dabar viskas. Problema išspręsta.

Atsakymas. $\left[ \begin(masyvas)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(masyvas) \right]$

Užduotis. Raskite atvirkštinę matricą:

\[\left[ \begin(masyvas)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(masyvas) \right] \]

Sprendimas. Dar kartą apskaičiuojame determinantą:

\[\begin(lygiuoti) & \left| \begin(masyvas)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(masyvas) \right|=\begin(matrica) ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrica)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(lygiuoti)\]

Determinantas nėra nulis - matrica yra apverčiama. Bet dabar bus tikrai sunku: turime suskaičiuoti net 9 (devynias, velnias!) algebrinius priedus. Ir kiekviename iš jų bus determinantas $\left[ 2\time 2 \right]$. Skraidė:

\[\begin(matrica) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrica) 2 & -1 \\ 0 & 1 \\\end(matrica) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrica) 0 & -1 \\ 1 & 1 \\\end(matrica) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrica) 0 & 2 \\ 1 & 0 \\\end(matrica) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrica) 1 & -1 \\ 0 & 2 \\\end(matrica) \right|=2; \\ \end(matrica)\]

Trumpai tariant, sąjungos matrica atrodys taip:

Taigi atvirkštinė matrica bus tokia:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrica) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\pabaiga(matrica) \right]=\left[ \begin(masyvas)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \2 & 1 & -2 \\\pabaiga (masyvas) \right]\]

Viskas. Štai atsakymas.

Atsakymas. $\left[ \begin(masyvas)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(masyvas) \right ]$

Kaip matote, kiekvieno pavyzdžio pabaigoje atlikome patikrinimą. Šiuo atžvilgiu svarbi pastaba:

Nepatingėkite patikrinti. Padauginkite pradinę matricą iš rastos atvirkštinės matricos – turėtumėte gauti $E$.

Atlikti šį patikrinimą yra daug lengviau ir greičiau, nei ieškoti klaidos tolesniuose skaičiavimuose, kai, pavyzdžiui, sprendžiate matricos lygtį.

Alternatyvus būdas

Kaip jau sakiau, atvirkštinės matricos teorema puikiai tinka dydžiams $\left[ 2\time 2 \right]$ ir $\left[ 3\time 3 \right]$ (in pastarasis atvejis- nebėra toks „nuostabus“), bet matricoms dideli dydžiai prasideda liūdesys.

Tačiau nesijaudinkite: yra alternatyvus algoritmas, su kuriuo galite ramiai rasti atvirkštinę vertę net matricai $\left[ 10\time 10 \right]$. Tačiau, kaip dažnai nutinka, norint apsvarstyti šį algoritmą, reikia šiek tiek teorinio įvado.

Elementarios transformacijos

Tarp visų galimų matricinių transformacijų yra keletas specialių – jos vadinamos elementariomis. Yra tiksliai trys tokios transformacijos:

Daugyba. Galite paimti $i$-ąją eilutę (stulpelį) ir padauginti ją iš bet kurio skaičiaus $k\ne 0$;
Papildymas. Prie $i$-os eilutės (stulpelio) pridėkite bet kurią kitą $j$-ąją eilutę (stulpelį), padaugintą iš bet kurio skaičiaus $k\ne 0$ (žinoma, galite padaryti $k=0$, bet kas yra esmė? Niekas nepasikeis).
Pertvarkymas. Paimkite $i$-ąją ir $j$-ąją eilutes (stulpelius) ir sukeiskite vietomis.

Kodėl šios transformacijos vadinamos elementariomis (didelėse matricose jos neatrodo tokios elementarios) ir kodėl jų yra tik trys – šie klausimai nepatenka į šios dienos pamokos sritį. Todėl į detales nesileisime.

Kitas dalykas yra svarbus: mes turime atlikti visus šiuos iškrypimus ant adjungtinės matricos. Taip, taip: teisingai girdėjote. Dabar bus dar vienas apibrėžimas – paskutinis šios dienos pamokoje.

Adjungtinė matrica

Žinoma, mokykloje jūs sprendėte lygčių sistemas sudavimo metodu. Na, iš vienos eilutės atimkite kitą, padauginkite kurią nors eilutę iš skaičiaus - viskas.

Taigi: dabar viskas bus taip pat, bet „suaugusiųjų“ būdu. Pasiruošę?

Apibrėžimas. Tegu pateikta matrica $A=\left[ n\times n \right]$ ir tapatumo matrica $E$ tokio pat dydžio $n$. Tada adjunktinė matrica $\left[ A\left| E\dešinė. \right]$ yra nauja $\left[ n\times 2n \right]$ dydžio matrica, kuri atrodo taip:

\[\left[ A\left| E\dešinė. \right]=\left[ \begin(masyvas)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(masyvas) \right]\]

Trumpai tariant, paimame matricą $A$, dešinėje jai priskiriame reikiamo dydžio tapatybės matricą $E$, jas atskiriame vertikalia juostele dėl grožio - štai jums adjunktas. :)

Koks laimikis? Štai kas:

Teorema. Tegul matrica $A$ yra apverčiama. Apsvarstykite adjungtinę matricą $\left[ A\left| E\dešinė. \right]$. Jei naudojate elementarios eilutės konversijos perkelkite jį į formą $\left[ E\left| B\right. \right]$, t.y. padauginus, atimant ir pertvarkant eilutes, kad iš $A$ gautumėte matricą $E$ dešinėje, tada kairėje gauta matrica $B$ yra atvirkštinė $A$:

\[\left[ A\left| E\dešinė. \dešinėn]\į \kairę[ E\kairė| B\right. \right]\Rightarrow B=((A)^(-1))\]

Tai taip paprasta! Trumpai tariant, atvirkštinės matricos paieškos algoritmas atrodo taip:

Parašykite adjungtinę matricą $\left[ A\left| E\dešinė. \right]$;
Atlikite elementarias eilutės konversijas, kol vietoj $A$ pasirodys $E$;
Žinoma, kažkas atsiras ir kairėje – tam tikra matrica $B$. Tai bus priešingai;
PELNAS! :)

Žinoma, tai daug lengviau pasakyti nei padaryti. Taigi pažvelkime į kelis pavyzdžius: dydžiams $\left[ 3\time 3 \right]$ ir $\left[ 4\time 4 \right]$.

Užduotis. Raskite atvirkštinę matricą:

\[\left[ \begin(masyvas)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(masyvas) \right]\ ]

Sprendimas. Sukuriame adjungtinę matricą:

\[\left[ \begin(masyvas)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 ir 1 \\\pabaiga (masyvas) \right]\]

Kadangi paskutinis pradinės matricos stulpelis užpildytas vienetais, pirmąją eilutę atimkite iš likusios:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\pabaiga (masyvas) \right]\begin (matrica) \downarrow \\ -1 \\ -1 \\\pabaiga (matrica)\į \\ & \į \kairę [ \begin(masyvas)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\pabaiga (masyvas) \right] \\ \end(lygiuoti)\]

Daugiau vienetų, išskyrus pirmąją eilutę, nėra. Bet mes jo neliečiame, kitaip naujai pašalinti vienetai pradės „daugintis“ trečiame stulpelyje.

Tačiau antrąją eilutę galime atimti du kartus iš paskutinės - vieną gauname apatiniame kairiajame kampe:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\pabaiga(masyvas) \right]\begin(matrica) \ \\ \downarrow \\ -2 \\\pabaiga(matrica)\į \\ & \left [ \begin(masyvas)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\pabaiga (masyvas) \right] \\ \end(lygiuoti)\]

Dabar galime atimti paskutinę eilutę iš pirmosios ir du kartus iš antrosios - tokiu būdu pirmąjį stulpelį „nuliuojame“:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(masyvas) \right]\begin(matrica) -1 \\ -2 \\ \uparrow \\\end(matrica)\į \\ & \ į \left[ \begin(masyvas)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(masyvas) \right] \\ \end(lygiuoti)\]

Antrąją eilutę padauginkite iš –1, tada iš pirmosios atimkite 6 kartus ir prie paskutinės pridėkite 1 kartą:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(masyvas) \right]\begin(matrica) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\pabaiga(matrica)\į \\ & \į \kairę[ \begin(masyvas)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(masyvas) \right]\begin(matrica) -6 \\ \rodyklė aukštyn žemyn \\ +1 \\\pabaiga (matrica)\į \\ & \į \kairę[ \begin(masyvas)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(masyvas) \right] \\ \end(lygiuoti)\]

Belieka sukeisti 1 ir 3 eilutes:

\[\left[ \begin(masyvas)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 ir 32 ir -13 \\\pabaiga (masyvas) \right]\]

Pasiruošę! Dešinėje yra reikiama atvirkštinė matrica.

Atsakymas. $\left[ \begin(masyvas)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(masyvas) \right ]$

Užduotis. Raskite atvirkštinę matricą:

\[\left[ \begin(matrica) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\pabaiga (matrica) \right]\]

Sprendimas. Dar kartą sudarome adjunktą:

\[\left[ \begin(masyvas)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(masyvas) \right]\]

Truputį verkkime, liūdėkime, kiek dabar turime suskaičiuoti... ir pradėkime skaičiuoti. Pirmiausia „nuliuokime“ pirmąjį stulpelį, iš 2 ir 3 eilučių atimdami 1 eilutę:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\pabaiga (masyvas) \right]\begin(matrica) \downarrow \\ -1 \\ -1 \\ \ \\\pabaiga(matrica)\to \\ & \to \left[ \begin (masyvas)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(masyvas) \right] \\ \end(lygiuoti)\]

Mes matome per daug "minusų" 2-4 eilutėse. Visas tris eilutes padauginkite iš –1, o trečiąjį stulpelį išdeginkite iš likusios 3 eilutę:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(masyvas) \right]\begin(matrica) \ \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\\pabaiga(matrica)\į \\ & \į \kairę[ \begin(masyvas)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ ? rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(masyvas) \right] \\ \end(lygiuoti)\]

Dabar pats laikas „kepti“ paskutinį pradinės matricos stulpelį: iš likusios atimkite 4 eilutę:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(masyvas ) \right]\begin(matrica) +1 \\ -3 \\ -2 \\ \uparrow \\\pabaiga(matrica)\į \\ & \į \kairę[ \begin(masyvas)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(masyvas) \right] \\ \end(lygiuoti)\]

Paskutinis metimas: „išdeginkite“ antrąjį stulpelį, iš 1 ir 3 eilučių atimant 2 eilutę:

\[\begin(lygiuoti) & \left[ \begin(masyvas)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end( masyvas) \right]\begin(matrica) 6 \\ \rodyklė aukštyn žemyn \\ -5 \\ \ \\\pabaiga(matrica)\į \\ & \į \kairę[ \begin(masyvas)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(masyvas) \right] \\ \end(lygiuoti)\]

Ir vėl tapatybės matrica yra kairėje, o tai reiškia, kad atvirkštinė yra dešinėje. :)

Atsakymas. $\left[ \begin(matrica) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\pabaiga (matrica) \right]$

Atvirkštinės matricos radimas- problema, kuri dažnai išsprendžiama dviem būdais:

algebrinių sudėjimų metodas, kai reikia rasti determinantus ir transponuoti matricas;
pašalinimo būdu nežinomas Gausas, kuriame reikia atlikti elementarias matricų transformacijas (sudėti eilutes, eilutes padauginti iš to paties skaičiaus ir pan.).

Tiems, kuriems ypač įdomu, yra ir kitų metodų, pavyzdžiui, tiesinių transformacijų metodas. Šioje pamokoje analizuosime tris minėtus atvirkštinės matricos radimo metodus ir algoritmus taikant šiuos metodus.

Atvirkštinė matrica A, tokia matrica vadinama

A
. (1)

Atvirkštinė matrica , kurią reikia rasti duotai kvadratinei matricai A, tokia matrica vadinama

kurio sandauga matricos A dešinėje yra tapatybės matrica, t.y.
. (1)

Tapatybės matrica yra įstrižainė, kurioje visi įstrižainės elementai yra lygūs vienetui.

Teorema.Kiekvienai nevienskaitinei (neišsigimusiai, ne vienaskaitinei) kvadratinei matricai galima rasti atvirkštinę matricą ir tik vieną. Specialiai (išsigimusiai, vienaskaitei) kvadratinei matricai atvirkštinė matrica neegzistuoja.

Kvadratinė matrica vadinama neypatingas(arba neišsigimęs, ne vienaskaita), jei jo determinantas nėra nulis, ir ypatingas(arba išsigimęs, vienaskaita), jei jo determinantas lygus nuliui.

Matricos atvirkštinę vertę galima rasti tik kvadratinei matricai. Natūralu, kad atvirkštinė matrica taip pat bus kvadratinė ir tokios pat eilės kaip ir duotoji matrica. Matrica, kuriai galima rasti atvirkštinę matricą, vadinama apverčiamąja matrica.

Dėl atvirkštinė matrica Yra atitinkama analogija su skaičiaus atvirkštine verte. Už kiekvieną skaičių a, nelygus nuliui, yra toks skaičius b kad darbas a Ir b lygus vienam: ab= 1. Skaičius b vadinamas atvirkštine skaičiaus b. Pavyzdžiui, skaičiaus 7 atvirkštinė vertė yra 1/7, nes 7*1/7=1.

Atvirkštinės matricos radimas naudojant algebrinių priedų metodą (sąjunginę matricą)

Ne vienaskaitos kvadratinei matricai A atvirkštinė yra matrica

kur yra matricos determinantas A, a yra matrica, susieta su matrica A.

Sujungta su kvadratine matrica A yra tos pačios eilės matrica, kurios elementai yra matricos determinanto atitinkamų elementų, perkeltų matricos A atžvilgiu, algebriniai papildiniai.

Tai

Atvirkštinės matricos radimo algoritmas naudojant algebrinių sudėjimų metodą

1. Raskite šios matricos determinantą A. Jei determinantas lygus nuliui, atvirkštinės matricos paieška sustoja, nes matrica yra vienaskaita, o atvirkštinė neegzistuoja.

2. Raskite matricą, transponuotą atžvilgiu A.

3. Apskaičiuokite sąjungos matricos elementus kaip 2 veiksme rasto marico algebrinius papildinius.

4. Taikykite (2) formulę: padauginkite atvirkštinę matricos determinanto vertę A, į sąjungos matricą, rastą 4 veiksme.

5. Padauginę šią matricą patikrinkite 4 veiksme gautą rezultatą Aį atvirkštinę matricą. Jei šių matricų sandauga yra lygi tapatybės matricai, tada atvirkštinė matrica buvo rasta teisingai. Priešingu atveju iš naujo pradėkite sprendimo procesą.

1 pavyzdys. Dėl matricos

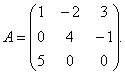
rasti atvirkštinę matricą.

Sprendimas. Norėdami rasti atvirkštinę matricą, turite rasti matricos determinantą A. Pagal trikampių taisyklę randame:

Todėl matrica A– ne vienaskaita (neišsigimęs, nevienskaita) ir jam yra atvirkštinė.

Raskime matricą, susietą su šia matrica A.

Raskime matricą, transponuotą matricos atžvilgiu A:

Sąjunginės matricos elementus apskaičiuojame kaip matricos, perkeltos matricos atžvilgiu, algebrinius papildinius A:

Todėl matrica susijungė su matrica A, turi formą

komentuoti. Elementų skaičiavimo ir matricos perkėlimo tvarka gali skirtis. Pirmiausia galite apskaičiuoti matricos algebrinius papildinius A, tada perkelkite algebrinio komplemento matricą. Rezultatas turėtų būti tie patys sąjungos matricos elementai.

Taikydami formulę (2), randame matricą atvirkštinę matricą A:

Atvirkštinės matricos radimas naudojant Gauso nežinomo eliminavimo metodą

Pirmasis žingsnis norint rasti atvirkštinę matricos vertę naudojant Gauso eliminavimo metodą yra priskirti matricą A tos pačios eilės tapatybės matrica, atskiriant jas vertikalia juosta. Gausime dvigubą matricą. Padauginkime abi šios matricos puses iš , tada gausime

Atvirkštinės matricos radimo algoritmas naudojant Gauso nežinomo eliminavimo metodą

1. Į matricą A priskirti tos pačios eilės tapatybės matricą.

2. Transformuokite gautą dvigubą matricą taip, kad jos kairėje pusėje gautumėte vienetinę matricą, tada dešinėje, vietoje tapatybės matricos, automatiškai gautumėte atvirkštinę matricą. Matrica A kairėje pusėje elementarios matricos transformacijomis paverčiama tapatybės matrica.

2. Jei matricos transformacijos procese A tapatybės matricoje bet kurioje eilutėje ar bet kuriame stulpelyje bus tik nuliai, tada matricos determinantas yra lygus nuliui, taigi ir matrica A bus vienaskaita ir neturi atvirkštinės matricos. Tokiu atveju tolesnis atvirkštinės matricos nustatymas sustoja.

2 pavyzdys. Dėl matricos

rasti atvirkštinę matricą.

ir transformuosime taip, kad kairėje pusėje gautume tapatybės matricą. Pradedame transformaciją.

Kairiosios ir dešiniosios matricos pirmąją eilutę padauginkite iš (-3) ir pridėkite prie antros eilės, o tada pirmąją eilutę padauginkite iš (-4) ir pridėkite prie trečios eilės, tada gausime

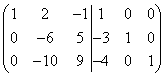Norėdami užtikrinti, kad vėlesnėse transformacijose nebūtų trupmeninių skaičių, pirmiausia sukurkime vienetą antroje eilutėje kairėje dvigubos matricos pusėje. Norėdami tai padaryti, padauginkite antrą eilutę iš 2 ir iš jos atimkite trečią eilutę, tada gausime

Sudėkime pirmąją eilutę su antrąja, o antrąją eilutę padauginkime iš (-9) ir pridėkime trečiąja eilute. Tada gauname

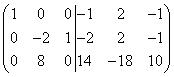Tada trečią eilutę padalinkite iš 8

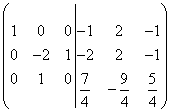Trečią eilutę padauginkite iš 2 ir pridėkite prie antrosios eilutės. Paaiškėja:

Sukeiskime antrąją ir trečiąją eilutes, tada galiausiai gausime:

Matome, kad kairėje pusėje turime tapatybės matricą, todėl dešinėje turime atvirkštinę matricą. Taigi:

Skaičiavimų teisingumą galite patikrinti padauginę pradinę matricą iš rastos atvirkštinės matricos:

Rezultatas turėtų būti atvirkštinė matrica.

3 pavyzdys. Dėl matricos

rasti atvirkštinę matricą.

Sprendimas. Dvigubos matricos sudarymas

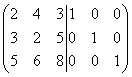
ir mes jį pakeisime.

Pirmą eilutę padauginame iš 3, o antrąją iš 2 ir atimame iš antrosios, tada padauginame pirmą eilutę iš 5, o trečią iš 2 ir atimame iš trečios eilutės, tada gauname

Pirmąją eilutę padauginame iš 2 ir pridedame prie antrosios, o tada iš trečios eilutės atimame antrąją, tada gauname

Matome, kad trečioje eilutėje kairėje pusėje visi elementai yra lygūs nuliui. Todėl matrica yra vienaskaita ir neturi atvirkštinės matricos. Mes nustojame toliau ieškoti atvirkštinio maritz.

Atvirkštinės matricos radimo metodai, . Apsvarstykite kvadratinę matricą

Pažymime Δ =det A.

Kvadratinė matrica A vadinama neišsigimęs, arba neypatingas, jei jo determinantas nėra lygus nuliui, ir išsigimęs, arba ypatingas, JeiΔ = 0.

Kvadratinė matrica B skirta tos pačios eilės kvadratinei matricai A, jei jų sandauga yra A B = B A = E, kur E yra tos pačios eilės tapatumo matrica kaip ir matricos A ir B.

Teorema . Kad matrica A turėtų atvirkštinę matricą, būtina ir pakanka, kad jos determinantas skirtųsi nuo nulio.

Matricos A atvirkštinė matrica, žymima A- 1, taigi B = A - 1 ir apskaičiuojamas pagal formulę

, (1)

kur A i j yra matricos A elementų a i j algebriniai papildiniai.

A -1 skaičiavimas naudojant (1) formulę aukštos eilės matricoms yra labai daug darbo reikalaujantis, todėl praktikoje patogu rasti A -1 elementariųjų transformacijų (ET) metodu. Bet kuri ne vienaskaita matrica A gali būti redukuota iki tapatybės matricos E, tapatybės matricai pritaikant tik stulpelius (arba tik eilutes). Jei per matricą A tobulos transformacijos ta pačia tvarka taikomos tapatybės matricai E, rezultatas bus atvirkštinė matrica. Patogu atlikti EP matricose A ir E vienu metu, abi matricas rašant viena šalia kitos per eilutę. Dar kartą pažymime, kad ieškant kanoninės matricos formos, norėdami ją rasti, galite naudoti eilučių ir stulpelių transformacijas. Jei reikia rasti atvirkštinę matricos vertę, transformavimo procese turėtumėte naudoti tik eilutes arba tik stulpelius.

2.10 pavyzdys. Dėl matricos rasti A-1.

Sprendimas.Pirmiausia randame matricos A determinantą
Tai reiškia, kad atvirkštinė matrica egzistuoja ir ją galime rasti naudodami formulę: , kur A i j (i,j=1,2,3) yra pradinės matricos elementų a i j algebriniai priedai.

Kur .

2.11 pavyzdys. Elementariųjų transformacijų metodu raskite matricos A -1: A = .

Sprendimas.Pradinei matricai dešinėje priskiriame tokios pat eilės tapatybės matricą: . Naudodami elementarias stulpelių transformacijas, kairiąją „pusę“ sumažinsime iki tapatybės, tuo pačiu atlikdami lygiai tokias pačias transformacijas dešinėje matricoje.
Norėdami tai padaryti, pakeiskite pirmąjį ir antrąjį stulpelius: ~ . Prie trečiojo stulpelio pridedame pirmąjį, o į antrąjį - pirmąjį, padaugintą iš -2: . Iš pirmo stulpelio atimame antrąjį padvigubintą, o iš trečiojo - antrąjį padaugintą iš 6; . Trečiąjį stulpelį pridėkime prie pirmojo ir antrojo: . Paskutinį stulpelį padauginkite iš -1: . Kvadratinė matrica, gauta dešinėje nuo vertikalios juostos, yra atvirkštinė duotosios matricos A matrica.
.