Koks yra optimalus pusiausvyros sprendimo mechanizmas. Pusiausvyros situacija

Pradedant spręsti problemą, pirmiausia reikėtų nustatyti nagrinėjamos sistemos (ypač mechanizmo) laisvės laipsnių skaičių pagal nepriklausomų galimų sistemos poslinkių ar koordinačių skaičių.

Plokštuminiuose mechanizmuose laisvės laipsnių skaičių praktiškai galima nustatyti taip. Įsivaizduokite, kad mechanizmas juda. Jei, sustabdę kurios nors vienos grandies transliacinį ar sukamąjį judėjimą, kartu sustabdome visą mechanizmą, tada jis turi vieną laisvės laipsnį. Jei po to dalis mechanizmo gali toliau judėti, bet sustabdžius kitos jungties judėjimą, mechanizmas sustoja, tada jis turi du laisvės laipsnius ir pan. Panašiai, jei mechanizmo padėtį nustatome pagal tam tikros koordinatės ir kai ji yra pastovi, mechanizmas negali judėti - jis turi vieną laisvės laipsnį. Jei po to dalis mechanizmo gali judėti, tada pasirenkama antroji koordinatė ir pan.

Norint išspręsti problemą geometriniu metodu, kai sistema turi vieną laisvės laipsnį, reikia: 1) pavaizduoti visas sistemą veikiančias aktyviąsias jėgas; 2) informuoti sistemą apie galimą judėjimą ir brėžinyje parodyti elementarius jėgų ar kampų taikymo taškų poslinkius 69, elementarius kūnų posūkius, kuriuos veikia jėgos (elementariesiems poslinkiams brėžinyje nurodysime jų modulius , kurie yra tiesiogiai įtrauktos į pusiausvyros sąlygas); 3) apskaičiuokite elementarų visų aktyviųjų jėgų darbą esant tam tikram poslinkiui pagal formules:

ir suformuluoti sąlygą (99); 4) nustatyti ryšį tarp dydžių, įtrauktų į lygybę (99), ir išreikšti šiuos dydžius kokiu nors vienetu, o tai visada galima padaryti vieno laisvės laipsnio sistemai.

Visus lygybės (99) dydžius pakeitę vienu, gauname lygtį, iš kurios galima rasti užduotyje ieškomą reikšmę arba priklausomybę.

Priklausomybes tarp galima rasti: a) iš atitinkamų geometrinių ryšių (164, 169 užduotys); b) iš kinematinių santykių, darant prielaidą, kad sistema juda, ir tam tikroje sistemos padėtyje, nustatant ryšį tarp atitinkamų sistemos taškų ar kūnų tiesinių arba kampinių greičių, o paskui darant prielaidą, kad tai tiesa, nes faktiniai poslinkiai, kuriuos gauna taškai ar kūnai per laiką, kai dt bus stacionariose grandyse, yra tarp galimų (kitaip čia galime iš karto laikyti, kad priklausomybės tarp galimų poslinkių yra tokios pat kaip ir tarp atitinkamų greičių, žr. 165 uždavinius, 166 ir kt.).

Sistemai su keliais laisvės laipsniais problemą galima išspręsti sudarant sąlygą (99) kiekvienam iš nepriklausomų galimų sistemos poslinkių ir transformuojant ją tokiu pačiu būdu. Dėl to sistema turės tiek pusiausvyros sąlygų, kiek ji turės laisvės laipsnių. Kitas sprendimo būdas, leidžiantis gauti tuos pačius rezultatus, yra nurodytas 144 straipsnyje.

Taikant analitinį skaičiavimo metodą, pusiausvyros sąlyga yra (100) formoje. Norėdami tai padaryti, pasirinkite koordinačių ašis, susijusias su kūnu, kuris, esant galimiems sistemos poslinkiams, lieka nejudantis. Tada apskaičiuojamos visų aktyviųjų jėgų projekcijos į pasirinktas ašis ir šių jėgų taikymo taškų koordinatės, išreiškiančios visas koordinates kokiu nors parametru (pavyzdžiui, kampu). Po to reikšmės randamos diferencijuojant koordinates šio parametro atžvilgiu.

Jei neįmanoma išreikšti visų koordinačių vienu parametru vienu metu, reikia įvesti kelis parametrus, o tada nustatyti ryšį tarp jų.

Apibendrinant pažymime, kad sąlygos (99) arba (100) gali būti naudojamos problemoms spręsti net esant trinčiai, įskaitant trinties jėgą aktyviųjų jėgų skaičiuje. Lygiai taip pat galima rasti suvaržymų reakcijas, jei, atmetę apribojimą, jį pakeisime atitinkama reakcija, pastarąją įtraukiame į aktyviųjų jėgų skaičių ir atsižvelgsime į tai, kad atmetus apribojimą suvaržymas, sistema įgauna naują laisvės laipsnį.

Uždavinys 164. Mechanizme, parodytame pav. 354, raskite ryšį tarp jėgų P ir Q pusiausvyroje.

Sprendimas, sistema turi vieną laisvės laipsnį. Jeigu sistemai pasakomas galimas judėjimas, tai visos strypų suformuotų lygiagretainių įstrižainės pailgės tiek pat. Tada .

Sudarę (99) lygtį, gauname:

kur . Rezultatas labai paprastas.

165 uždavinys. Rąsto Q svoris, kiekvieno iš dviejų cilindrinių ritinėlių, ant kurių jis pastatytas, svoris P. Nustatykite, kokia jėga F turi būti veikiamas rąstas, kad jis išlaikytų pusiausvyrą pasvirusioje plokštumoje duotas pasvirimo kampas a (355 pav.). Ritinėlių trintis ant plokštumos ir rąsto užtikrina, kad nebūtų slydimo.

Sprendimas. Jei nepaisoma pasipriešinimo riedėjimui, tada ritinėlių plokštuma bus ideali jungtis. Riedant neslystant sistema turi vieną laisvės laipsnį. Pasakydami sistemai apie galimą poslinkį, gauname pagal sąlygą (99)

kur galimas rąsto poslinkis, sutampantis su taško B poslinkiu.

Sąlyčio taškas K yra momentinis čiuožimo greičių centras. Todėl, jei apsvarstysime , Pakeitę šią reikšmę į ankstesnę lygtį, pagaliau rasime

Užduotis 166. Raskite ryšį tarp momento M poros, veikiančios švaistiklio-slankiklio mechanizmo švaistiklį (356 pav.) ir slėgio jėgos P stūmoklį pusiausvyros būsenoje, jei

Sprendimas. Mechanizmas turi vieną laisvės laipsnį. Iš pusiausvyros sąlygos (99), jei įdėsime, gausime:

Sprendimas sumažinamas iki ryšio tarp Ši kinematinė problema buvo išspręsta anksčiau (žr. § 57, 63 uždavinį). Naudodami ten gautą rezultatą, randame

167 uždavinys. 83 uždavinyje nagrinėjamai pavarų dėžei (žr. § 70) raskite ryšį tarp pavaros velenui A taikomo sukimo momento ir varomajam velenui B veikiančio pasipriešinimo momento, kai abu velenai sukasi tolygiai.

Sprendimas. Tolygiai sukantis, santykis tarp bus toks pat kaip ir esant pusiausvyrai. Todėl pagal sąlygą (99), jei įdėsime:

Vadinasi, naudodami 83 uždavinyje gautą rezultatą, randame

168 uždavinys

Sprendimas. Sudarę pusiausvyros sąlygą (99), gauname

Daroma prielaida, kad vienodai sukant rankeną, tada ir tolygiai atsukamas svirtis

Pakeitę šią reikšmę į ankstesnę lygybę, randame

Atkreipiame dėmesį, kad šios paprastos problemos išvis nepavyko išspręsti geometrinės statikos metodais, nes mechanizmo detalės nėra žinomos.

Išspręstas uždavinys parodo, kokios (iš esmės) yra taikomo metodo galimybės. Tačiau atliekant konkretų tokio mechanizmo inžinerinį skaičiavimą, žinoma, reikės atsižvelgti į trintį tarp jo dalių, todėl reikės žinoti, koks yra mechanizmas.

169 uždavinys. Sija, susidedanti iš dviejų sijų, sujungtų vyriais C, neša apkrovą P (358 pav., a). Sijos matmenys ir atramų vieta nurodyti brėžinyje. Nustatykite slėgio jėgą atramai B, kurią sukelia tam tikra apkrova.

Sprendimas. Atramą B išmetame ir pakeičiame reakcija N in, skaičiais lygi norimai slėgio jėgai (358 pav., b). Informavę sistemą apie galimą judėjimą (dabar ji turi vieną laisvės laipsnį), sudarome sąlygą (99)

Mes nustatome ryšį tarp proporcijų:

Vadinasi,

Taikant geometrinės statikos metodą, sprendimas pasirodytų ilgesnis (reikėtų atsižvelgti į pluošto dalių pusiausvyrą ir įvesti papildomas kitų apribojimų reakcijas, o vėliau šias reakcijas išskirti iš gautos pusiausvyros sistemos lygtys).

170 uždavinys. Horizontalus strypas 1 su svarmeniu, pritvirtintu taške A vyriais (359 pav.), vyriais B sujungtas su strypu 2, kurio svoris yra C galas, strypas remiasi į horizontalias grindis, sudarydamas kampu su juo a. Nustatykite, kokiai vertei sijos trinties jėga grindyse bus sistemos pusiausvyra.

Sprendimas. Pavaizduojame sistemą veikiančias jėgas ir trinties jėgą F, įtraukiant ją į aktyviųjų jėgų skaičių; šiuo atveju jėgą išskaidome į dvi dedamąsias, kurių kiekviena yra lygi ir taikoma taškuose B ir C (atkreipiame dėmesį į šią techniką, kuri labai palengvina galimo darbo skaičiavimą).

Sudarę pusiausvyros sąlygą (99) ir atsižvelgdami į formules (101), gauname pažymėdami

Bet, pagal analogiją su teorema dėl dviejų kūno taškų greičių projekcijų, , Kur . Tada ir galiausiai

Atkreipkite dėmesį, kad šioje užduotyje, naudojant geometrinės statikos metodus, neįmanoma sudaryti tik vienos lygties, iš kurios iš karto būtų galima rasti F.

171 uždavinys. Planetiniame mechanizme su diferencine pavara (žr. § 70) ant ašies A yra nepriklausomai pritvirtinta spindulio krumpliaratis 1 ir švaistiklis AB, laikantis spindulio krumpliaračio 2 ašį B (pav. 360). Sukimo momentas M veikia švaistiklį, o pasipriešinimo momentai – 1 ir 2 pavaras. Raskite vertes esant mechanizmo pusiausvyrai.

Optimalios strategijos konfliktų teorijoje yra tos strategijos, kurios veda žaidėjus į stabilią pusiausvyrą, t.y. kai kurios situacijos, kurios tenkina visus žaidėjus.

Žaidimo teorijos sprendimo optimalumas grindžiamas koncepcija pusiausvyros situacija:

1) nė vienam žaidėjui neapsimoka nukrypti nuo pusiausvyros situacijos, jei joje lieka visi kiti,

2) pusiausvyros prasmė – pakartotinai kartojant žaidimą žaidėjai pasieks pusiausvyros situaciją, pradėdami žaidimą bet kurioje strateginėje situacijoje.

Kiekvienoje sąveikoje gali būti šių tipų pusiausvyros:

1. pusiausvyra atsargiose strategijose . Nulemta strategijų, kurios suteikia žaidėjams garantuotą rezultatą;

2. pusiausvyra dominuojančiose strategijose .

Dominuojanti strategija yra toks veiksmų planas, kuris suteikia dalyviui didžiausią naudą, nepaisant kito dalyvio veiksmų. Todėl dominuojančių strategijų pusiausvyra bus abiejų žaidimo dalyvių dominuojančių strategijų sankirta.

Jei žaidėjų optimalios strategijos dominuoja visose kitose jų strategijose, tada žaidime yra dominuojančių strategijų pusiausvyra. Kalinio dilemos žaidime Nash pusiausvyros strategijų rinkinys bus („pripažink – pripažink“). Be to, svarbu pažymėti, kad ir žaidėjui A, ir žaidėjui B dominuojanti strategija yra „atpažinti“, o „neatpažinti“ dominuoja;

3. pusiausvyra Nešas . Nešo pusiausvyra yra dviejų ar daugiau žaidėjų žaidimo sprendimo tipas, kuriame joks dalyvis negali padidinti laimėjimo vienašališkai pakeisdamas savo sprendimą, kai kiti dalyviai nekeičia savo sprendimo.

Tarkime, žaidimas nįprastos formos veidai, kur yra grynųjų strategijų rinkinys ir išmokų rinkinys.

Kai kiekvienas žaidėjas pasirenka strategiją strategijų profilyje, žaidėjas gauna laimėjimą. Be to, atsipirkimas priklauso nuo viso strategijų profilio: ne tik nuo paties žaidėjo pasirinktos strategijos, bet ir nuo kitų žmonių strategijų. Strategijos profilis yra Nash pusiausvyra, jei strategijos pakeitimas nėra naudingas jokiam žaidėjui, ty jokiam

Žaidimas gali turėti Nash pusiausvyrą tiek grynoje, tiek mišrioje strategijoje.

Nashas tai įrodė, jei buvo leista mišrios strategijos, tada kiekviename žaidime nžaidėjai turės bent vieną Nešo pusiausvyrą.

Nash pusiausvyros situacijoje kiekvieno žaidėjo strategija suteikia jam geriausią atsaką į kitų žaidėjų strategijas;

4. Balansas Stackelbergas. Stackelbergo modelis– žaidimo teorinis oligopolinės rinkos modelis, esant informacijos asimetrijai. Šiame modelyje įmonių elgsena apibūdinama dinamišku žaidimu su visa tobula informacija, kuriame firmų elgsena modeliuojama naudojant statinisžaidimai su visa informacija. Pagrindinis žaidimo bruožas yra pirmaujančios įmonės buvimas, kuri pirmiausia nustato prekių produkcijos apimtį, o likusios įmonės vadovaujasi tuo apskaičiuodamos. Pagrindinės žaidimo sąlygos:

Pramonė gamina vienalytę prekę: skirtingų firmų produkcijos skirtumai yra nežymūs, vadinasi, pirkėjas, rinkdamasis, iš kurios firmos pirkti, orientuojasi tik į kainą;

Pramonėje yra nedaug įmonių.

firmos nustato pagaminamos produkcijos kiekį, o jo kaina nustatoma pagal paklausą;

Yra vadinamoji lyderė, kurios gamybos apimtimi vadovaujasi kitos įmonės.

Taigi, Stackelberg modelis naudojamas ieškant optimalaus sprendimo dinaminiuose žaidimuose ir atitinka maksimalų žaidėjų atsipirkimą, remiantis sąlygomis po vieno ar kelių žaidėjų jau padaryto pasirinkimo. Stackelbergo pusiausvyra.- situacija, kai nė vienas iš žaidėjų negali vienašališkai padidinti savo laimėjimo, o sprendimus pirmiausia priima vienas žaidėjas, o antrasis tampa žinomas. Kalinio dilemos žaidime Stackelbergo pusiausvyra bus pasiekta aikštėje (1; 1) – abiejų nusikaltėlių „pripažinti kaltę“;

5. Pareto optimalumas- tokia sistemos būsena, kai kiekvieno konkretaus kriterijaus, apibūdinančio sistemos būklę, reikšmė negali būti pagerinta nepabloginant kitų žaidėjų padėties.

Pareto principas teigia: „Bet koks pokytis, kuris neatneša nuostolių, bet yra naudingas kai kuriems žmonėms (jų pačių vertinimu), yra patobulinimas. Taigi pripažįstama teisė į visus pakeitimus, kurie niekam nedaro papildomos žalos.

Sistemos būsenų, kurios yra Pareto optimalios, rinkinys vadinamas „Pareto aibė“, „Pareto optimalių alternatyvų rinkinys“ arba „optimalių alternatyvų rinkinys“.

Situacija, kai buvo pasiektas Pareto efektyvumas, yra situacija, kai išnaudota visa mainų nauda.

Pareto efektyvumas yra viena iš pagrindinių šiuolaikinės ekonomikos sąvokų. Remiantis šia koncepcija, sukonstruojamos pirmoji ir antroji pagrindinės gerovės teoremos.

Vienas iš Pareto optimalumo pritaikymų yra Pareto išteklių (darbo ir kapitalo) paskirstymas tarptautinėje ekonominėje integracijoje, t.y. dviejų ar daugiau valstybių ekonominė sąjunga. Įdomu tai, kad Pareto pasiskirstymas prieš ir po tarptautinės ekonominės integracijos buvo tinkamai aprašytas matematiškai (Dalimov R.T., 2008). Analizė parodė, kad sektorių pridėtinė vertė ir darbo resursų pajamos juda priešingomis kryptimis pagal gerai žinomą šilumos laidumo lygtį, panašiai kaip dujos ar skystis erdvėje, kas leidžia pritaikyti naudojamą analizės techniką. fizikoje, susijusioje su ekonominėmis ekonominių parametrų migracijos problemomis.

Pareto optimalus teigia, kad visuomenės gerovė pasiekia maksimumą, o išteklių paskirstymas tampa optimalus, jei bet koks šio pasiskirstymo pokytis pablogina bent vieno ekonominės sistemos subjekto gerovę.

Pareto-optimali rinkos būklė- situacija, kai neįmanoma pagerinti kurio nors ekonominio proceso dalyvio padėties, tuo pačiu nesumažinant bent vieno iš kitų gerovės.

Pagal Pareto kriterijų (socialinės gerovės augimo kriterijų) judėjimas link optimalumo galimas tik tokiu resursų paskirstymu, kuris padidina bent vieno žmogaus gerovę, nepakenkiant niekam kitam.

Situacija S* laikoma Pareto dominuojančia situacija S, jei:

bet kuriam žaidėjui jo atlyginimas S<=S*

· yra bent vienas žaidėjas, kuriam jo išmokėjimas situacijoje S*>S

„Kalinių dilemos“ problemoje Pareto pusiausvyra, kai neįmanoma pagerinti nė vieno žaidėjo padėties nepabloginant kito padėties, atitinka aikštės situaciją (2; 2).

Apsvarstykite 1 pavyzdys:

Pusiausvyra dominuojančiose strategijose ne.

Nešo pusiausvyra. (5.5) ir (4.4). Kadangi vienam iš žaidėjų individualiai nukrypti nuo pasirinktos strategijos yra nenaudinga.

Pareto optimalus. (5.5). Kadangi žaidėjų atsipirkimas renkantis šias strategijas yra didesnis nei atlygis renkantis kitas strategijas.

Stackelbergo pusiausvyra:

Žaidėjas A atlieka pirmąjį ėjimą.

Pasirenka savo pirmąją strategiją. B pasirenka pirmąją strategiją. A gauna 5.

Pasirinko antrąją strategiją. B pasirenka antrąjį. A gauna 4.

5 > 4 =>

B žengia pirmą žingsnį.

Pasirenka savo pirmąją strategiją. A pasirenka pirmąją strategiją. B gauna 5.

Pasirinko antrąją strategiją. Ir jis pasirenka antrąjį. B gauna 4.

5 > 4 => Stackelbergo pusiausvyra (5, 5)

2 pavyzdysduopolijos modeliavimas.

Apsvarstykite šio modelio esmę:

Tebūnie pramonė su dviem firmomis, iš kurių viena yra „vadovaujanti įmonė“, o kita – „pasekančioji įmonė“. Tegul produkto kaina yra tiesinė visos pasiūlos funkcija K:

P(K) = a − bQ.

Taip pat darykime prielaidą, kad įmonių kaštai produkcijos vienetui yra pastovūs ir lygūs iš 1 ir iš 2 atitinkamai. Tada pirmosios firmos pelną lems formulę

Π 1 = P(K 1 + K 2) * K 1 − c 1 K 1 ,

ir atitinkamai antrojo pelno

Π 2 = P(K 1 + K 2) * K 2 − c 2 K 2 .

Pagal Stackelberg modelį pirmoji įmonė – pirmaujanti įmonė – pirmiausia priskiria savo produkciją K vienas . Po to antroji firma – sekanti įmonė – analizuodama lyderiaujančios įmonės veiksmus nustato jos produkciją. K 2. Abiejų firmų tikslas yra maksimaliai padidinti savo mokėjimo funkcijas.

Nešo pusiausvyrą šiame žaidime lemia atgalinė indukcija. Apsvarstykite priešpaskutinį žaidimo etapą – antrosios firmos žingsnį. Šiame etape 2 įmonė žino optimalų 1 įmonės našumą K vienas*. Tada optimalios produkcijos nustatymo problema K 2 * yra sumažintas iki problemos, kaip rasti maksimalų antrosios įmonės išmokėjimo funkcijos tašką, sprendimą. Funkcijos Π 2 maksimizavimas kintamojo atžvilgiu K 2 skaičiavimas K 1, mes nustatome, kad optimali antrosios įmonės produkcija

Tai geriausias sekančios įmonės atsakymas į lyderės įmonės pasirinkimą K vienas*. Pirmaujanti įmonė gali maksimaliai padidinti savo atsipirkimo funkciją, atsižvelgdama į funkcijos formą K 2*. Maksimalus funkcijos Π 1 taškas kintamajame K 1 pakeičiant K 2 * valia

Pakeičiant tai išraiška for K 2 * , mes gauname

Taigi, esant pusiausvyrai, pirmaujanti įmonė pagamina dvigubai daugiau produkcijos nei sekanti įmonė.

Panagrinėkime rinkos pusiausvyros nustatymo mechanizmą, kai, veikiama pasiūlos ar paklausos veiksnių pokyčių, rinka išeina iš šios būsenos. Yra du pagrindiniai pasiūlos ir paklausos disproporcijos variantai: prekių perteklius ir trūkumas.

Perteklius Prekės (perteklius) – situacija rinkoje, kai prekės pasiūla tam tikra kaina viršija jos paklausą. Šiuo atveju vyksta konkurencija tarp gamintojų, kova dėl pirkėjų. Laimi tas, kuris pasiūlo palankesnes prekių pardavimo sąlygas. Taigi rinka linkusi grįžti į pusiausvyros būseną.

trūkumas prekės – tokiu atveju už prekes už nurodytą kainą reikalaujamas kiekis viršija siūlomą kiekį. Šioje situacijoje tarp pirkėjų jau kyla konkurencija dėl galimybės įsigyti ribotą prekę. Laimi tas, kuris pasiūlo didžiausią šios prekės kainą. Padidėjusi kaina patraukia gamintojų dėmesį, kurie pradeda plėsti gamybą, taip didindami prekių pasiūlą. Dėl to sistema grįžta į pusiausvyros būseną.

Taigi kaina atlieka balansavimo funkciją, skatindama plėsti gamybą ir prekių, kurių trūkumas yra, tiekimą ir riboja pasiūlą, išlaisvindama rinką nuo pertekliaus.

Balansuojantis kainos vaidmuo pasireiškia tiek per paklausą, tiek per pasiūlą.

Tarkime, kad mūsų rinkoje nusistovėjusi pusiausvyra sutriko – veikiant bet kokiems veiksniams (pavyzdžiui, pajamų augimui) padidėjo paklausa, dėl to jos kreivė pasislinko nuo D1 in D2(4.3 a pav.), o pasiūlymas liko nepakitęs.

Jei tam tikros prekės kaina nepasikeitė iš karto po paklausos kreivės poslinkio, tai po paklausos augimo susidarys situacija, kai ankstesne kaina P1 prekių kiekis, kurį dabar gali kiekvienas iš pirkėjų pirkimas (QD) viršija apimtį, kurią tam tikra kaina gali pasiūlyti tam tikros prekės gamintojai prekės (QS). Paklausos dydis dabar viršys šio produkto pasiūlą, o tai reiškia, kad prekių trūkumas kursu Df = QD – Qsšioje rinkoje.

Prekių trūkumas, kaip jau žinome, lemia pirkėjų konkurenciją dėl galimybės įsigyti šią prekę, o tai lemia rinkos kainų augimą. Pagal pasiūlos dėsnį, pardavėjų reakcija į kainos padidėjimą bus siūlomų prekių kiekio padidėjimas. Diagramoje tai bus išreikšta rinkos pusiausvyros taško judėjimu E1 išilgai pasiūlos kreivės, kol susikerta su nauja paklausos kreive D2 kur bus pasiekta nauja tam tikros rinkos pusiausvyra E2 s pusiausvyros prekių kiekis Q2 ir pusiausvyros kaina P2.

Ryžiai. 4.3. Pusiausvyros kainos taško poslinkis.

Apsvarstykite situaciją, kai pasiūlos pusėje bus pažeista pusiausvyros būsena.

Tarkime, kad dėl kai kurių veiksnių padidėjo pasiūla, dėl kurios jos kreivė pasislinko į dešinę iš padėties S1 in S2 o paklausa išliko nepakitusi (4.3 pav. b).

Kol rinkos kaina išliks ta pati (R1) pasiūlos padidėjimas sukels perteklius prekių dydžio Sp = Qs–QD. Dėl to yra pardavėjų konkurencija, dėl ko mažėja rinkos kaina (su P1 prieš P2) ir parduotų prekių kiekio padidėjimas. Diagramoje tai atsispindės rinkos pusiausvyros taško judėjime E1 išilgai paklausos kreivės, kol ji susikerta su nauja pasiūlos kreive, todėl susidaro nauja pusiausvyra E2 su parametrais Q2 Ir P2.

Panašiai galima nustatyti paklausos mažėjimo ir pasiūlos sumažėjimo poveikį pusiausvyrinei kainai ir prekių pusiausvyriniam kiekiui.

Mokomojoje literatūroje suformuluotos keturios pasiūlos ir paklausos sąveikos taisyklės.

1. Paklausos padidėjimas sukelia pusiausvyros kainos ir prekių pusiausvyros kiekio padidėjimą.

2. Sumažėjus paklausai, sumažėja ir prekių pusiausvyros kaina, ir pusiausvyrinis kiekis.

3. Pasiūlos padidėjimas reiškia pusiausvyros kainos sumažėjimą ir pusiausvyros prekių kiekio padidėjimą.

4. Pasiūlos sumažėjimas reiškia pusiausvyros kainos padidėjimą ir pusiausvyros prekių kiekio sumažėjimą.

Naudodami šias taisykles galite rasti bet kokių pasiūlos ir paklausos pokyčių pusiausvyros tašką.

Šios aplinkybės daugiausia gali trukdyti kainai grįžti į rinkos pusiausvyros lygį:

1) administracinis kainų reguliavimas

2) monopolija gamintojas ar vartotojas, leidžiantis išlaikyti monopolinę kainą, kuri gali būti dirbtinai aukšta arba žema.

| | Pagrindiniai dualumo teorijos apibrėžimai.

Kiekviena linijinio programavimo problema gali būti susieta su kita linijinio programavimo problema. Išsprendus vieną iš jų, automatiškai išsprendžiama kita problema. Tokios užduotys vadinamos abipusiai dvejopomis. Parodykime, kaip, atsižvelgiant į pateiktą problemą (vadinsime ją pradine), galime sukurti jos dualą.

Apsvarstykite planuojamos produkcijos problemą.

F = 3 X 1 + 5X 2 + 4X 3 + 5X 4 → maks.
5x1 +0,4x2 +2x3 +0,5x4 ≤400
5x2 +x3 +x4 ≤300
x 1 + x 3 + x 4 ≤100
x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0, x 4 ≥ 0

Bendrosios dvigubos problemos sudarymo taisyklės:

Tiesiai	dvigubas
Tikslinė funkcija (maks.)	Dešinė apribojimų pusė
Dešinė apribojimų pusė	Tikslinė funkcija (min.)
A – apribojimo matrica	A T – apribojimo matrica
i-asis apribojimas: ≤ 0, (≥ 0)	Kintamasis y i ≥ 0, (≤ 0)
i-asis apribojimas: = 0	Kintamasis y i ≠ 0
Kintamasis x j ≥ 0 (≤ 0)
Kintamasis x j ≠ 0	j-asis apribojimas: = 0

maks. → min

Tiesiai	dvigubas
Tikslinė funkcija (min.)	Dešinė apribojimų pusė
Dešinė apribojimų pusė	Tikslinė funkcija (maks.)
A – apribojimo matrica	A T – apribojimo matrica
i-asis apribojimas: ≥ 0, (≤ 0)	Kintamasis y i ≥ 0, (≤ 0)
i-asis apribojimas: = 0	Kintamasis y i ≠ 0
Kintamasis x j ≥ 0 (≤ 0)	j-asis apribojimas: ≤ 0 (≥ 0)
Kintamasis x j ≠ 0	j-asis apribojimas: = 0

Sukurkime jos dvigubą problemą pagal šias taisykles.

1. Kintamųjų skaičius dviguboje užduotyje yra lygus nelygybių skaičiui pradinėje užduotyje.
2. Dvigubo uždavinio koeficientų matrica perkeliama į pradinės problemos koeficientų matricą.
3. Pradinio uždavinio laisvųjų terminų stulpelis yra dvigubos tikslo funkcijos koeficientų eilutė. Tikslinė funkcija yra maksimaliai padidinta vienoje problemoje, o sumažinama kitoje.
4. Pirminės problemos kintamųjų neneigiamumo sąlygos atitinka kita kryptimi nukreiptus dualinės problemos nelygybes-ribojimus. Ir atvirkščiai, suvaržymo nelygybės originale atitinka dualo neneigiamumo sąlygas.

Atkreipkite dėmesį, kad I užduoties matricos eilutės yra II užduoties matricos stulpeliai. Todėl II uždavinio kintamųjų y i koeficientai yra atitinkamai I uždavinio i-osios nelygybės koeficientai.
Gautas modelis yra ekonominis ir matematinis problemos modelis, susietas su tiesiogine problema.

Nelygybės, sujungtos rodyklėmis, bus skambučio konjugatas.
Prasmingas dvigubos problemos formulavimas: suraskite tokią išteklių Y = (y 1 , y 2 ..., ym) kainų (įverčių) aibę, kuriai esant bendra išteklių kaina bus minimali, su sąlyga, kad išteklių sąnaudos kiekvienos rūšies gamyboje produkto bus ne mažiau kaip pelnas ( pajamos iš šių produktų pardavimo.
Išteklių kainos y 1 , y 2 ..., y m ekonominėje literatūroje gavo įvairius pavadinimus: apskaitinė, numanoma, šešėlinė. Šių pavadinimų reikšmė yra ta, kad tai yra sąlyginės, „netikros“ kainos. Priešingai nei „išorinės“ produktų kainos nuo 1 , nuo 2 ..., nuo n, paprastai žinomos prieš pradedant gamybą, išteklių y 1, y 2 ..., ym kainos yra vidinės. , nes jie nustatomi ne iš išorės, o nustatomi tiesiogiai sprendžiant problemą, todėl dažnai vadinami išteklių įvertinimais.
Ryšys tarp tiesioginių ir dvejopų problemų visų pirma susideda iš to, kad vienos iš jų sprendimas gali būti gaunamas tiesiogiai sprendžiant kitą.

Dualumo teoremos

Dvilypumas yra pagrindinė linijinio programavimo teorijos sąvoka. Pagrindiniai dualumo teorijos rezultatai yra dviejose teoremose, vadinamose dualumo teoremomis.

Pirmoji dvilypumo teorema.

Jei viena iš dviejų I ir II uždavinių poros yra sprendžiama, tai kita yra išsprendžiama, o objektyvių funkcijų reikšmės optimaliuose planuose yra vienodos, F(x*) = G(y*), kur x *, y * - optimalūs I ir II uždavinių sprendimai

Antroji dvilypumo teorema.

Planai x * ir y * yra optimalūs I ir II uždaviniuose tada ir tik tada, kai juos atitinkamai pakeitus į I ir II uždavinių apribojimų sistemą, bent viena iš bet kurios konjuguotų nelygybių poros tampa lygybe.
Tai fundamentalioji dvilypumo teorema. Kitaip tariant, jei x * ir y * yra įmanomi pirminių ir dvigubų uždavinių sprendimai, o jei c T x*=b T y*, tai x * ir y * yra optimalūs dvigubų uždavinių poros sprendimai.

Trečioji dvilypumo teorema. Kintamųjų y i reikšmės optimaliame dvigubos problemos sprendime yra apribojimų sistemos laisvųjų narių b i - tiesioginės problemos nelygybės - įtakos šios problemos objektyvios funkcijos vertei:
Δf(x) = b i y i

Išspręsdami LLP simplekso metodu, tuo pačiu metu išsprendžiame ir dvigubą LLP. Dvigubos problemos y i kintamųjų reikšmės optimaliame plane vadinamos objektyviai nustatytais arba dvigubais įverčiais. Taikomuose uždaviniuose dvigubi įverčiai y i dažnai vadinami paslėptomis, šešėlinėmis kainomis arba ribinių išteklių įvertinimais.

Abipusių dvejopų problemų savybė

1. Viename uždavinyje ieškoma tiesinės funkcijos maksimumo, kitoje – minimumo.
2. Vienos problemos tiesinės funkcijos kintamųjų koeficientai yra laisvieji apribojimų sistemos nariai kitoje.
3. Kiekviena iš uždavinių pateikta standartine forma, o maksimizavimo uždavinyje visos formos nelygybės ≤ , o minimizavimo uždavinyje visos formos nelygybės ≥ .
4. Abiejų uždavinių apribojimų sistemų kintamųjų koeficientų matricos perkeliamos viena į kitą:
5. Nelygybių skaičius vienos problemos apribojimų sistemoje yra toks pat, kaip ir kitos problemos kintamųjų skaičius.
6. Abiejose problemose yra kintamųjų neneigiamumo sąlygos.

Pusiausvyros teorema

2 užduotis
Sukurkite dvigubą uždavinį 1 uždaviniui. Raskite jį sprendimas pagal pusiausvyros teoremą.
3x1 +x2 ≥12
x1 +2x2 ≥14
4x1 +11x2 ≥68

Pusiausvyros teorema . Tegul X*=(x 1 *,...,x n *) ir Y*=(y 1 *,...,y n *) yra leistini simetriškos formos dvigubų uždavinių modeliai. Šie planai yra optimalūs, jei ir tik tenkinamos šios papildomos laisvumo sąlygos: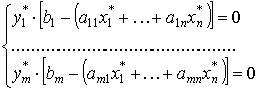


4 teorema leidžia mums nustatyti optimalų vienos iš dvejopų uždavinių poros sprendimą, sprendžiant kitą. Jei vienos problemos apribojimas tampa griežta nelygybe, kai pakeičiamas optimalus sprendimas, tai atitinkamas dvigubas kintamasis optimaliame dvigubos problemos sprendime yra lygus 0. Jei bet kuris kintamasis yra teigiamas optimaliame vienos problemos plane, tada atitinkamas dvigubos problemos apribojimas yra lygtis.
Pateiksime ekonominį komplementarinio tingumo sąlygų aiškinimą. Jei optimaliame sprendime kai kurios žaliavos įvertis yra kitoks nei 0, tada ji bus visiškai išnaudota (resursų yra mažai). Jeigu žaliava nevisiškai sunaudota (yra perteklius), tai jos įvertinimas lygus 0. Taigi gauname, kad dvejopi vertinimai yra žaliavų trūkumo matas. Įvertis parodo, kiek tikslo funkcijos reikšmė padidės, atitinkamos žaliavos atsargoms padidėjus 1 vienetu. Jei tam tikros rūšies gaminys yra įtrauktas į gamybos planą, tai jo gamybos savikaina sutampa su pagamintos prekės savikaina. Jeigu prekės pagaminimo kaštai yra didesni už prekės savikainą, tai prekė negaminama.
Jei vienoje iš dvigubų uždavinių poros yra du kintamieji, ją galima išspręsti grafiškai, o tada, naudojant 3 ir 4 teoremas, rasti dvigubos problemos sprendimą. Tokiu atveju gali kilti 3 atvejai: abi problemos turi įmanomus sprendimus, tik viena turi įmanomus sprendimus, abi problemos neturi įmanomų sprendimų.

2 pavyzdys
Sudarykite dvigubą uždavinį ir raskite jos sprendimą, naudodami pusiausvyros teoremą
x 2 -2x 3 +2x 4 -2x 5 ≤4
-2x 1 -2x 2 +2x 3 +2x 4 +x 5 ≥2
x i ≥0, i=1,5
Z=10x 1 -9x 2 -19x 3 -13x 4 -11x 5 → max, jei žinomas pradinės problemos sprendimas: Zmax=(3;4;0;0;0).
Sukurkime dvigubą problemą. Nelygybės požymius sutinkame su pradinės problemos tikslu.

Z = 10x 1 -9x 2 -19x 3 -13x 4 -11x 5 → maks.
Dviguba užduotis:

W=4 m. 1 -2 m. 2 → min
Raskime optimalų dvigubo uždavinio sprendimą naudodamiesi pusiausvyros teorema. Užrašykime komplementarinio laisvumo sąlygas.
y 1 (4-(x 2 -2x 3 +2x 4 -2x 5)) = 0
y 2 (-2-(2x 1 -2x 2 -2x 3 -2x 4 -x 5)) = 0
x 1 (-2y 2 -10) = 0
x 2 (y 1 -2y 2 +9) = 0
x 3 (-2y 1 -2y 2 +19) = 0
x 4 (2 m. 1 - 2 m. 2 +13) = 0
x 5 (-2y 1 -y 2 +11) = 0
Sukompiliuota sistema pakeisime optimalų pradinio uždavinio sprendimą: x 1 =3, x 2 =4, x 3 =0, x 4 =0, x 5 =0.
y 1 (4-(4-2 0+2 0-2 0)) = 0
y 2 (-2-(2 3-2 4-2 0-2 0-0)) = 0 W(y 1 , y 2 , y 3) = 12y 1 +31y 2 +18y 3 → maks. Pagal 3 teoremą Zmax=Wmin=100000.
Galiausiai Wmin=W(0; 4000/7; 32000/21) = 100000

Galimų poslinkių principo taikymas

Galimų poslinkių principas labai efektyvus tiriant plokščiųjų mechanizmų pusiausvyrą, t.y. tokie, kurių grandys juda plokštumose, lygiagrečiomis kokiai nors fiksuotai plokštumai. Supaprastinus, galime daryti prielaidą, kad visi jo taškai ir nuorodos juda išilgai paties piešinio plokštumos.

Atsižvelgiant į tai, kad visos mechanizmo grandžių jungtys, kaip ir išorinės jungtys, yra idealios, jų reakcijas neįtraukiame. Tai lemia galimų poslinkių principo pranašumus lyginant su geometrinės statikos metodais (pusiausvyros lygtimis).

Nepaisydami trinties, raskite ryšį tarp jėgų P Ir K, kuriame švaistiklio-slankiklio mechanizmas bus pusiausvyroje, jei jėga yra statmena OA(2.8 pav.).

Informavęs galimo judėjimo mechanizmą ir prilyginęs nuliui jėgų darbo sumą P Ir K apie šį poslinkį gauname

P× dS B – Q×dS A = 0,

kur dS A Ir dS B– galimų taškų poslinkių moduliai BET Ir IN.

juda dS A statmenai OA, dS B nukreiptas tiesia linija OB. Norint nustatyti ryšį tarp dS B Ir dS A raskite nuorodos MKC AB.Jis yra statmenų ir galimų taškų poslinkių krypčių sankirtoje BET Ir IN. Šie judesiai priklauso nuo taškų greičio BET Ir IN, t.y.

Įvedus kampų žymėjimą j Ir y, iš sinuso teoremos randame

Priklausomybė tarp galimų judesių dS A Ir dS B galima nustatyti naudojant taško greičio projekcijos teoremą A Ir B tiesiogiai AB. Šią teoremą galima parašyti:

dS A cos = dS B× jaukus,

Nagrinėjama problema galėtų būti išspręsta naudojant standžiosios kėbulo statikos metodus. Norėdami tai padaryti, turite sudaryti kiekvienos mechanizmo grandies pusiausvyros lygtis (alkūnę OA, švaistiklis AB, skaitytuvas IN); šiuo atveju reikėtų atsižvelgti į nežinomas jungčių reakcijas (vyrių reakcijas BET Ir IN ir kreiptuvų, kuriuose juda slankiklis, reakcija).

Sprendžiant tokio pobūdžio problemas, akivaizdus galimų poslinkių principo pranašumas; šis metodas leidžia neįtraukti nežinomų ryšių reakcijos, nes šios reakcijos nėra įtrauktos į sistemos pusiausvyros sąlygą, išreikštą galimų poslinkių principu.

2.6. Galimų poslinkių principo taikymas

prie ryšių reakcijų apibrėžimo

Reakcijos jėgų formuluojant galimų poslinkių principą neatsiranda. Tačiau šioms jėgoms nustatyti galima efektyviai taikyti galimų poslinkių principą ir kuo sudėtingesnė konstrukcija, tuo didesnis galimų poslinkių principo pranašumas, lyginant su geometrinėje statikoje naudojamais metodais (pusiausvyros lygčių sudarymas ir sprendimas). .

Statinės konstrukcijos (struktūros) turi nulinį mobilumo laipsnį, t.y. yra subalansuoti dėl išorinių ir vidinių santykių buvimo. Ryšys standaus tvirtinimo pavidalu, uždėtas ant kūno, riboja bet kokius jo judesius, todėl reakcija vaizduojama dviejų komponentų, nukreiptų išilgai koordinačių ašių, ir reaktyvaus momento pavidalu. Šarnyrinė fiksuota atrama riboja kūno judėjimą dviem tarpusavyje statmenomis kryptimis, jo reakcija vaizduojama kaip du komponentai išilgai koordinačių ašių.

Taikant atpalaidavimo nuo jungčių principą, galima atmesti vieną ryšį, kuris riboja kūno judėjimą viena kryptimi, pakeičiant jį reakcijos jėga.

Tais atvejais, kai suvaržymas neleidžia kūnui judėti keliomis kryptimis (fiksuota šarnyrinė atrama, standus tvirtinimas), jis pakeičiamas kito tipo suvaržymu, leidžiančiu judėti reakcijos, kurią norime nustatyti, kryptimi.

Norint nustatyti reaktyvųjį momentą standžiajame tvirtinimo elemente, jis pakeičiamas fiksuota šarnyrine atrama ir norimu reaktyviniu momentu (2.9 pav.).

Norint nustatyti horizontalią arba vertikalią standžiojo įterpimo reakcijos dedamąją, ji pakeičiama tipo strypo sujungimu kreiptuvuose ir norima reakcija (2.10, 2.11 pav.).

Tokiu būdu galima nuosekliai nustatyti visų ryšių reakcijas. Tokiu atveju kiekvieną kartą atmetamas ryšys, kurio reakciją reikia nustatyti, ir mechaninė sistema gauna vieną laisvės laipsnį.

Tais atvejais, kai jungtis neleidžia kėbului judėti keliomis kryptimis (fiksuota šarnyrinė atrama, standus tvirtinimas), jis nėra visiškai išmetamas, o tik pakeičiamas paprastesniu. Kaip tai daroma, parodyta fig. 2.12.

Nustatydami jo reakcijas parodysime šarnyrinės fiksuotos atramos pakeitimo galimybes.

Apsvarstykite kompozito palaikymo reakcijų nustatymo pavyzdžius
struktūros.