Apibrėžkite funkcijos grafiko įstrižąją asimptotę. Kiek asimptotų gali turėti funkcijos grafikas?

Kiek asimptotų gali turėti funkcijos grafikas?

Nėra, vienas, du, trys... arba begalinis skaičius. Ieškodami pavyzdžių toli nenueisime, priminsime elementarias funkcijas. Parabolė, kubinė parabolė, sinusoidas visai neturi asimptotų. Eksponentinės, logaritminės funkcijos grafikas turi vieną asimptotę. Arktangentas, arkotangentas, turi du iš jų, o liestinė, kotangentas turi begalinį skaičių. Neretai grafikas turi ir horizontalias, ir vertikalias asimptotes. Hiperbolė, visada tave mylėsiu.

Ką reiškia rasti funkcijos grafiko asimptotes?

Tai reiškia, kad reikia išsiaiškinti jų lygtis ir nubrėžti tiesias linijas, jei to reikalauja problemos sąlyga. Procesas apima funkcijos ribų nustatymą.

Funkcijos grafiko vertikaliosios asimptotės

Vertikali grafiko asimptotė, kaip taisyklė, yra funkcijos begalinio nenuoseklumo taške. Tai paprasta: jei taške funkcija patiria begalinį lūžį, tai lygties nurodyta tiesė yra vertikali grafiko asimptotė.

Pastaba: atkreipkite dėmesį, kad žymėjimas naudojamas dviem visiškai skirtingoms sąvokoms nurodyti. Taškas yra numanomas arba tiesės lygtis - priklauso nuo konteksto.

Taigi, norint nustatyti vertikalios asimptotės buvimą taške, pakanka parodyti, kad bent viena iš vienpusių ribų yra begalinė. Dažniausiai tai yra taškas, kuriame funkcijos vardiklis yra lygus nuliui. Tiesą sakant, paskutiniuose pamokos apie funkcijos tęstinumą pavyzdžiuose jau radome vertikalias asimptotes. Tačiau daugeliu atvejų yra tik viena vienpusė riba, o jei ji begalinė, tai vėlgi – meilė ir palankumas vertikaliajai asimptotei. Paprasčiausia iliustracija: ir y ašis.

Iš to, kas pasakyta, taip pat išplaukia akivaizdus faktas: jei funkcija nuolat įjungta, vertikalių asimptočių nėra. Kažkodėl į galvą atėjo parabolė. Iš tiesų, kur čia galima „klijuoti“ tiesią liniją? ... taip ... suprantu ... dėdės Freudo pasekėjai glaudėsi isterikoje =)

Atvirkštinis teiginys paprastai nėra teisingas: pavyzdžiui, funkcija nėra apibrėžta visoje realioje eilutėje, tačiau iš jos visiškai atimta asimptočių.

Funkcijos grafiko pasvirosios asimptotės

Pasvirusios (ypatingu atveju – horizontalios) asimptotes galima nubrėžti, jei funkcijos argumentas linkęs į „plius begalybė“ arba „minus begalybė“. Todėl funkcijos grafikas negali turėti daugiau nei 2 pasvirusias asimptotes. Pavyzdžiui, eksponentinės funkcijos grafikas turi vieną horizontalią asimptotę ties, o lanko liestinės at grafikas turi dvi tokias asimptotes ir skirtingas.

Hiperbolė yra taškų, kurių atstumo skirtumas iki dviejų nurodytų taškų, vadinamų židiniais, lokusas yra pastovi reikšmė (ši konstanta turi būti teigiama ir mažesnė už atstumą tarp židinių).

Šią konstantą pažymėkime 2a, atstumą tarp židinių pažymėkime ir koordinačių ašis parinksime taip pat, kaip § 3. Tegul yra savavališkas hiperbolės taškas.

Pagal hiperbolės apibrėžimą

Dešinėje lygybės pusėje turite pasirinkti pliuso ženklą jei ir minuso ženklą, jei

Kadangi paskutinė lygybė gali būti parašyta taip:

Tai hiperbolės lygtis pasirinktoje koordinačių sistemoje.

Išsilaisvinę nuo radikalų šioje lygtyje (kaip § 3), galime lygtį redukuoti iki paprasčiausios formos.

Perkeldami pirmąjį radikalą į dešinę lygybės pusę ir padalydami abi puses kvadratu, po akivaizdžių transformacijų gauname:

Dar kartą padalijus abi lygybės puses kvadratu, sumažinus panašius dėmenis ir padalinus iš laisvojo termino, gauname:

Nuo , vertė yra teigiama. Žymėdami jį per , t.y. nustatymą

gauname kanoninę hiperbolės lygtį.

Mes tiriame hiperbolės formą.

1) Hiperbolės simetrija. Kadangi (3) lygtyje yra tik dabartinių koordinačių kvadratai, koordinačių ašys yra hiperbolės simetrijos ašys (žr. analogišką elipsės teiginį). Hiperbolės, ant kurios yra židiniai, simetrijos ašis vadinama židinio ašimi. Simetrijos ašių susikirtimo taškas – simetrijos centras – vadinamas hiperbolės centru. Hiperbolės, pateiktos pagal (3) lygtį, židinio ašis sutampa su Ox ašimi, o pradžia yra centras.

2) Susikirtimo taškai su simetrijos ašimis. Raskite hiperbolės susikirtimo taškus su simetrijos ašimis – hiperbolės viršūnes. Darant prielaidą, kad lygtyje randame hiperbolės susikirtimo su ašimi taškų abscises

Todėl taškai yra hiperbolės viršūnės (51 pav.); atstumas tarp jų yra 2a. Norėdami rasti susikirtimo taškus su Oy ašimi, įdedame lygtį Gauname lygtį šių taškų ordinatėms nustatyti

y., mes gavome įsivaizduojamas reikšmes; tai reiškia, kad y ašis nekerta hiperbolių.

Atsižvelgiant į tai, simetrijos ašis, kuri kerta hiperbolę, vadinama tikrąja simetrijos ašimi (židinio ašimi), simetrijos ašis, kuri nesikerta su hiperbolėmis, vadinama įsivaizduojama simetrijos ašimi. Hiperbolės, pateiktos (3) lygtimi, tikroji simetrijos ašis yra ašis, įsivaizduojama simetrijos ašis – ašis Atkarpa, jungianti hiperbolės viršūnes, taip pat jos ilgis 2a, vadinama tikrąja simetrijos ašimi. hiperbolė. Jei įsivaizduojamoje hiperbolės simetrijos ašyje abiejose jos centro O pusėse išdėstytos atkarpos OB, kurių ilgis b, tai atkarpa ir jos ilgis vadinami įsivaizduojama hiperbolės ašimi. Dydžiai a ir b vadinami atitinkamai tikrosiomis ir įsivaizduojamomis hiperbolės pusašimis.

3) Hiperbolės forma. Tiriant hiperbolės formą, pakanka atsižvelgti į teigiamas x ir y reikšmes, nes kreivė yra simetriškai išdėstyta koordinačių ašių atžvilgiu.

Kadangi iš (3) lygties matyti, kad 1, tai jis gali kisti nuo a iki Kai jis didėja nuo a iki tada Y taip pat didėja nuo 0 iki Kreivės forma parodyta Fig. 51. Jis yra už juostos, apribotos tiesiomis linijomis, ir susideda iš dviejų atskirų atšakų. Bet kuriam vienos iš šių šakų taškui M (dešinė šaka), bet kuriam kitos šakos taškui M (kairė šaka).

4) Hiperbolės asimptotės. Norėdami aiškiau įsivaizduoti hiperbolės formą, apsvarstykite dvi tiesias linijas, glaudžiai susijusias su ja - vadinamąsias asimptotes.

Darant prielaidą, kad x ir y yra teigiami, išsprendžiame (3) hiperbolės lygtį y ordinatės atžvilgiu:

Palyginkime lygtį su tiesės lygtimi, atitinkamai įvardydami du taškus, esančius atitinkamai šioje tiesėje ir hiperbolėje ir turinčius tą pačią abscisę (51 pav.). Akivaizdu, kad skirtumas Y – atitinkamų taškų ordinatėse išreiškia atstumą tarp jų, t.y.

Parodykime, kad atstumui MN didėjant neribotai, kai jis žudo, jis linkęs į nulį. Iš tikrųjų,

Supaprastinus gauname:

Iš paskutinės formulės matome, kad neribotai padidėjus abscisei, atstumas MN mažėja ir linkęs į nulį. Iš to išplaukia, kad kai taškas M, judėdamas išilgai hiperbolės pirmajame kvadrante, tolsta iki begalybės, tada jo atstumas iki tiesės mažėja ir linksta į nulį. Ta pati aplinkybė atsitiks, kai taškas M judės išilgai hiperbolės trečiajame kvadrante (dėl simetrijos apie pradžią O).

Galiausiai dėl hiperbolės simetrijos Oy ašies atžvilgiu gausime antrą tiesę, simetriškai išsidėsčiusią su tiesia linija, prie kurios taškas M taip pat neribotai artės judėdamas išilgai hiperbolės ir toldamas į begalybę ( antrajame ir ketvirtame kvadrantuose).

Šios dvi tiesės vadinamos hiperbolės asimptotėmis ir, kaip matėme, turi lygtis:

Akivaizdu, kad hiperbolės asimptotės yra išilgai stačiakampio įstrižainių, kurių viena kraštinė lygiagreti Ox ašiai ir lygi 2a, kita lygiagreti Oy ašiai ir lygi, o centras yra pradžioje ( žr. 51 pav.).

Braižant hiperbolę pagal jos lygtį, pirmiausia rekomenduojama sukonstruoti jos asimptotes.

Lygiakraščio hiperbolė. Hiperbolės atveju vadinama lygiakraštė; jos lygtis gaunama iš (3) ir turi tokią formą:

Akivaizdu, kad lygiakraštės hiperbolės asimptočių nuolydžiai bus Todėl lygiakraštės hiperbolės asimptotės yra statmenos viena kitai ir dalija kampus tarp jos simetrijos ašių.

Daugeliu atvejų nubraižyti funkciją yra lengviau, jei pirmiausia nubraižote kreivės asimptotes.

Apibrėžimas 1. Asimptotėmis vadinamos tokios tiesės, prie kurių funkcijos grafikas priartėja tiek, kiek norima, kai kintamasis linkęs į plius begalybę arba minus begalybę.

Apibrėžimas 2. Tiesė vadinama funkcijos grafiko asimptote, jei atstumas nuo kintamojo taško M funkcijos grafikas iki šios linijos linkęs į nulį, nes taškas neribotai tolsta M nuo koordinačių pradžios išilgai bet kurios funkcijos grafiko šakos.

Yra trys asimptotų tipai: vertikalūs, horizontalūs ir įstrižai.

Vertikalios asimptotės

Apibrėžimas. Tiesiai x = a yra funkcijos grafiko vertikali asimptote jei taškas x = a yra antrojo tipo lūžio taškasšiai funkcijai.

Iš apibrėžimo matyti, kad eilutė x = a yra funkcijos grafiko vertikali asimptotė f(x), jei tenkinama bent viena iš šių sąlygų:

Tuo pačiu metu funkcija f(x) gali būti visiškai neapibrėžtas, atitinkamai, už x ≥ a ir x ≤ a .

Komentuoti:

1 pavyzdys Funkcijų grafikas y=ln x turi vertikalią asimptotę x= 0 (t. y. sutampa su ašimi Oy) ant apibrėžimo srities ribos, nes funkcijos riba kaip x linkusi į nulį dešinėje yra lygi minus begalybei:

(pav. aukščiau).

savarankiškai ir tada pamatysite sprendimus

2 pavyzdys Raskite funkcijos grafiko asimptotes.

3 pavyzdys Raskite funkcijos grafiko asimptotes

Horizontalios asimptotės

If (funkcijos riba, kai argumentas linkęs į pliusą arba minusą begalybę, yra lygi tam tikrai reikšmei b), tada y = b – horizontalioji asimptote kreivas y = f(x ) (dešinė, kai x linkusi į pliuso begalybę, kairė, kai x linkusi į minus begalybę, ir dvipusė, jei ribos, kai x linkusios į pliuso arba minus begalybę, yra lygios).

5 pavyzdys Funkcijų grafikas

adresu a> 1 turi kairę horizontalią asimptotę y= 0 (t. y. sutampa su ašimi Jautis), nes funkcijos riba, kai "x" linkusi į minus begalybę, yra lygi nuliui:

Kreivė neturi dešinės horizontalios asimptotės, nes funkcijos riba kaip x linkusi plius begalybė yra lygi begalybei:

Įstrižai asimptotai

Vertikalios ir horizontalios asimptotės, kurias nagrinėjome aukščiau, yra lygiagrečios koordinačių ašims, todėl joms sukurti reikėjo tik tam tikro skaičiaus - abscisės arba ordinačių ašies taško, per kurį eina asimptotė. Daugiau reikia įstrižai asimptotei – nuolydžiui k, kuris rodo tiesės pasvirimo kampą ir sankirtą b, kuris rodo, kiek linija yra aukščiau arba žemiau pradžios. Tie, kurie neturėjo laiko pamiršti analitinės geometrijos, o iš jos - tiesės lygčių, pastebės, kad įstrižai asimptotei jie randa nuolydžio lygtis. Įstrižinės asimptotės egzistavimą lemia tokia teorema, kurios pagrindu randami ką tik įvardyti koeficientai.

Teorema. Norėdami padaryti kreivę y = f(x) turėjo asimptotą y = kx + b , būtina ir pakanka, kad egzistuotų baigtinės ribos k ir b nagrinėjamos funkcijos, nes kintamasis linkęs x iki begalybės ir minus begalybės:

(1)

(2)

Taip rasti skaičiai k ir b ir yra pasvirosios asimptotės koeficientai.

Pirmuoju atveju (kai x linkęs į plius begalybę) gaunama dešinioji pasviroji asimptotė, antruoju (kai x linkusi į minus begalybę) paliekama. Dešinysis įstrižas asimptotas parodytas Fig. iš apačios.

Ieškant įstrižosios asimptotės lygties, reikia atsižvelgti į x tendenciją ir į plius begalybę, ir į minus begalybę. Kai kurioms funkcijoms, pavyzdžiui, trupmeninėms racionalijoms, šios ribos sutampa, tačiau daugeliui funkcijų šios ribos skiriasi ir gali egzistuoti tik viena.

Kai ribos sutampa su x linkusiu į plius begalybę ir minus begalybę, tiesi linija y = kx + b yra dvipusė kreivės asimptotė.

Jei bent viena iš asimptotą apibrėžiančių ribų y = kx + b , neegzistuoja, tada funkcijos grafikas neturi pasvirosios asimptotės (bet gali turėti vertikalią).

Nesunku pastebėti, kad horizontali asimptotė y = b yra ypatingas įstrižo atvejis y = kx + b adresu k = 0 .

Todėl, jei kreivė turi horizontalią asimptotę bet kuria kryptimi, tai įstriosios asimptotės ta kryptimi nėra ir atvirkščiai.

6 pavyzdys Raskite funkcijos grafiko asimptotes

Sprendimas. Funkcija apibrėžta visoje skaičių eilutėje, išskyrus x= 0, t.y.

Todėl lūžio taške x= 0 kreivė gali turėti vertikalią asimptotę. Iš tikrųjų funkcijos, kaip x linkęs į nulį iš kairės, riba yra plius begalybė:

Vadinasi, x= 0 yra šios funkcijos grafiko vertikali asimptotė.

Šios funkcijos grafikas neturi horizontalios asimptotės, nes funkcijos riba, kai x linkusi į plius begalybę, yra lygi plius begalybei:

Išsiaiškinkime įstrižos asimptotės buvimą:

Turi ribotas ribas k= 2 ir b= 0. Tiesiai y = 2x yra dvipusė įstrižinė šios funkcijos grafiko asimptotė (pav. pavyzdžio viduje).

7 pavyzdys Raskite funkcijos grafiko asimptotes

Sprendimas. Funkcija turi vieną lūžio tašką x= –1 . Apskaičiuokime vienpuses ribas ir nustatykime nutrūkimo tipą:

Išvada: x= −1 yra antrojo tipo nutrūkimo taškas, taigi linija x= −1 yra šios funkcijos grafiko vertikali asimptotė.

Ieškote įstrižų asimptotų. Kadangi ši funkcija yra šiek tiek racionali, už ir už ribos sutaps. Taigi, mes randame koeficientus, kaip pakeisti tiesią liniją - įstrižą asimptotę į lygtį:

Rastus koeficientus pakeitę tiesės su nuolydžiu lygtimi, gauname įstrižosios asimptotės lygtį:

y = −3x + 5 .

Paveiksle funkcijos grafikas pažymėtas bordo spalva, o asimptotės – juodos spalvos.

8 pavyzdys Raskite funkcijos grafiko asimptotes

Sprendimas. Kadangi ši funkcija yra ištisinė, jos grafikas neturi vertikalių asimptočių. Mes ieškome įstrižų asimptotų:

.

Taigi šios funkcijos grafikas turi asimptotę y= 0 ties ir neturi asimptoto ties .

9 pavyzdys Raskite funkcijos grafiko asimptotes

Sprendimas. Pirmiausia ieškome vertikalių asimptočių. Norėdami tai padaryti, randame funkcijos domeną. Funkcija apibrėžiama, kai nelygybė galioja ir . kintamasis ženklas x atitinka ženklą. Todėl apsvarstykite ekvivalentinę nelygybę . Iš to gauname funkcijos apimtį: . Vertikali asimptotė gali būti tik ant funkcijos srities ribos. Bet x= 0 negali būti vertikali asimptotė, nes funkcija yra apibrėžta x = 0 .

Apsvarstykite dešinės pusės ribą ties (kairės ribos nėra):

.

Taškas x= 2 yra antrojo tipo nutrūkimo taškas, taigi linija x= 2 – šios funkcijos grafiko vertikali asimptotė.

Mes ieškome įstrižų asimptotų:

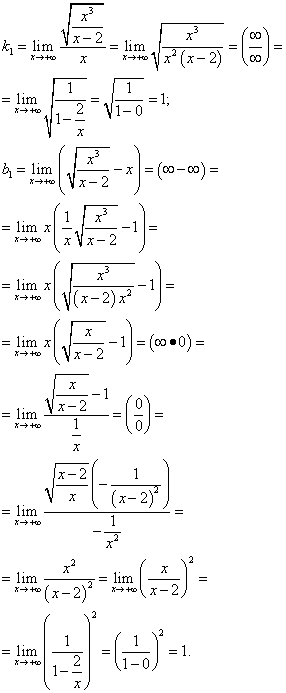
Taigi, y = x+ 1 - šios funkcijos grafiko pasvirusi asimptotė ties . Mes ieškome įstrižos asimptotės:

Taigi, y = −x − 1 - įstrižas asimptotas ties .

10 pavyzdys Raskite funkcijos grafiko asimptotes

Sprendimas. Funkcija turi taikymo sritį . Kadangi šios funkcijos grafiko vertikali asimptotė gali būti tik ant apibrėžimo srities ribos, tai funkcijos vienpuses ribas rasime ties .

Kaip svetainėje įterpti matematines formules?

Jei kada nors prireiks prie tinklalapio pridėti vieną ar dvi matematines formules, paprasčiausias būdas tai padaryti yra taip, kaip aprašyta straipsnyje: matematinės formulės lengvai įterpiamos į svetainę paveikslėlių, kuriuos Wolfram Alpha automatiškai generuoja, pavidalu. Be paprastumo, šis universalus metodas padės pagerinti svetainės matomumą paieškos sistemose. Jis veikia jau seniai (ir, manau, veiks amžinai), bet morališkai pasenęs.

Kita vertus, jei savo svetainėje nuolat naudojate matematines formules, rekomenduoju naudoti MathJax – specialią JavaScript biblioteką, kuri rodo matematinius žymėjimus žiniatinklio naršyklėse, naudojant MathML, LaTeX arba ASCIIMathML žymėjimą.

Yra du būdai pradėti naudoti MathJax: (1) naudodami paprastą kodą, prie savo svetainės galite greitai prijungti MathJax scenarijų, kuris bus automatiškai įkeltas iš nuotolinio serverio reikiamu metu (serverių sąrašas); (2) Įkelkite MathJax scenarijų iš nuotolinio serverio į savo serverį ir prijunkite jį prie visų savo svetainės puslapių. Antrasis metodas yra sudėtingesnis ir reikalaujantis daug laiko ir leis jums pagreitinti jūsų svetainės puslapių įkėlimą, o jei pagrindinis MathJax serveris dėl kokių nors priežasčių laikinai taps nepasiekiamas, tai neturės jokios įtakos jūsų svetainei. Nepaisant šių privalumų, pasirinkau pirmąjį būdą, nes jis paprastesnis, greitesnis ir nereikalaujantis techninių įgūdžių. Sekite mano pavyzdžiu ir per 5 minutes savo svetainėje galėsite naudotis visomis MathJax funkcijomis.

Galite prijungti MathJax bibliotekos scenarijų iš nuotolinio serverio naudodami dvi kodo parinktis, paimtas iš pagrindinės MathJax svetainės arba iš dokumentacijos puslapio:

Vieną iš šių kodo parinkčių reikia nukopijuoti ir įklijuoti į savo tinklalapio kodą, geriausia tarp žymų ir arba iškart po žymos . Pagal pirmąjį variantą MathJax įkeliamas greičiau ir mažiau sulėtina puslapį. Tačiau antroji parinktis automatiškai seka ir įkelia naujausias MathJax versijas. Jei įterpsite pirmąjį kodą, jį reikės periodiškai atnaujinti. Jei įklijuosite antrą kodą, puslapiai bus įkeliami lėčiau, tačiau jums nereikės nuolat stebėti MathJax atnaujinimų.

Lengviausias būdas prijungti „MathJax“ yra „Blogger“ arba „WordPress“: svetainės valdymo skydelyje pridėkite valdiklį, skirtą trečiosios šalies „JavaScript“ kodui įterpti, nukopijuokite į jį pirmąją arba antrąją aukščiau pateikto įkėlimo kodo versiją ir įdėkite valdiklį arčiau. į šablono pradžią (beje, tai visai nebūtina, nes MathJax scenarijus įkeliamas asinchroniškai). Tai viskas. Dabar išmokite MathML, LaTeX ir ASCIIMathML žymėjimo sintaksę ir būsite pasiruošę į savo tinklalapius įdėti matematines formules.

Bet koks fraktalas statomas pagal tam tikrą taisyklę, kuri nuosekliai taikoma neribotą skaičių kartų. Kiekvienas toks laikas vadinamas iteracija.

Iteratyvus Menger kempinės konstravimo algoritmas yra gana paprastas: originalus kubas su 1 kraštine plokštumos, lygiagrečios jo paviršiams, padalintas į 27 vienodus kubus. Iš jo pašalinamas vienas centrinis kubas ir 6 šalia jo esantys kubeliai. Pasirodo rinkinys, susidedantis iš 20 likusių mažesnių kubelių. Tą patį padarę su kiekvienu iš šių kubelių, gauname rinkinį, kurį sudaro 400 mažesnių kubelių. Tęsdami šį procesą neribotą laiką, gauname Menger kempinę.